中考数学总复习涉及初中三年学习的所有内容，知识点多，题型多，盲目地做题并不理智，而且是无效的;而对众多的题型进行分类归纳，总结出每类题型在变化中不变的因素或共性，才是真正提高解题效率及数学成绩的途径之一。

　　以归纳“多解题”为例来说明如何进行题型分类归纳。

　　为避免在中考“多解题”中出现“漏解”的情况，同学们可以对初中几何不同的知识模块中出现的“多解题”进行归纳总结。部分举例如下：

　　一.圆中“多解题”举例

　　(一)圆与圆的位置关系;

　　举例1.两个没有公共点的圆半径分别为1cm和3cm，求两圆的圆心距d的取值范围?(相离包括外离和内含)

　　2、两圆相切，半径分别是3和7，求两圆的圆心距?(相切包括外切和内切)

　　(二)弦(非直径)所对的弧是优弧或劣弧;

　　举例1、△ABC内接于⊙O，∠AOB=120°，求∠ACB?(点C在优弧上或在劣弧上)

　　2.PA，PC分别切⊙O于A，C两点，B为⊙O上与A，C不重合的点，若∠P=40°，求∠ABC?(点B在优弧上或在劣弧上)

　　3、△ABC是半径为2cm的圆内接三角形，若BC=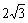

cm，求∠A的度数。(BC所对的是优弧或劣弧)

　　(三)位置关系的不确定

　　举例1、平面上一点到圆的最大距离、最小距离分别是7和3，求圆的直径。(点在圆外或在圆内)

　　2、圆的两条平行弦长6和8，半径5，求两条弦的距离。(两条弦在圆心的同侧或异侧)

　　二、三角形中“多解题”举例

　　(一)等腰三角形

　　举例：1、等腰三角形两边长7和9，求周长。(底是7或9)

　　2、等腰三角形的一个外角是125°，求它的顶角的大小?

　　(125°是顶角的外角或底角的外角)