无锡中考网整理：

　　中考新题型旋转变换的证明四招搞定：近几年各地课改区的中考试题中出现了一种新题型—旋转题，它常是以动态的形式出现，将一个图形或其部分绕某一个点旋转一定的角度产生新的图形，从中探求结论。

　　旋转的三要素：旋转中心、旋转角度、旋转方向

　　解题关键：旋转前后的图形全等。

　　下面结合中考试题，分析如下，以帮助同学们学习这类问题．

　　【例1】（益阳）如图1，桌面内，直线l上摆放着两块大小相同的直角三角板，它们中较小直角边的长为6cm，较小锐角的度数为30°.

　　(1)将△ECD沿直线AC翻折到如图1（a）的位置，与AB相交于点F，请证明：

　　（2）将△ECD沿直线l向左平移到1（b）的位置，使E点落在AB上，你可以求出平移的距离，试试看：

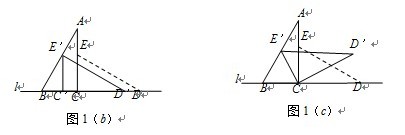
　　（3）将△ECD绕点C逆时针方向旋转到图1（c）的位置，使E点落在AB上，请求出旋转角的度数.

　　【解析】（1）根据轴反射的性质可知，在△AFE与△FB中，

　　∵∠A＝∠，AE＝B，∠AFE＝∠FB，

　　∴△AFE≌△FB

　　∴AF＝F

　　（2）根据平移的性质可知为平移的距离.在Rt△中，，

　　所以

　　（3）根据旋转的性质可知，△为等边三角形，∠为旋转角.

　　∴旋转角∠为30°.

　　【点评】本题以同学们熟悉的两块三角板为背景，设计了翻折（也就是是绕C点旋转）、平移、旋转三种变换，由此引发出图形变换后的线段大小的证明、平移距离的探索及旋转角度的大小．三个小问分别是并列式问题，但在探究过程中，抓住本题三角板是30度、60度的特殊三角板对分析问题帮助很大．

　　【例2】（遂宁）如图2，把正方形ACFG与Rt△ACB按如图（甲）所示重叠在一起，其中AC=2，∠BAC=60°，若把Rt△ACB绕直角顶点C按顺时针方向旋转，使斜边AB恰好经过正方形ACFG的顶点F，得△A′B′C′，AB分别与A′C、A′B′相交于点D、E，如图（乙）所示．

　　问：△ABC至少旋转多少度才能得到△A′B′C′？说明理由；

　　【解析】∵ACGF是正方形，A‘B′经过点F，∴A′C=CF．

　　又·∵∠A′=60°∴△A′CF是等边三角形

　　∵∠A′CF=60°∴∠ACA′=90°一60°=30°

　　∴△ABC至少旋转30°才能得到△A′CB′

　　【点评】本题通过原来部分重叠在一起的正方形ACFG与Rt△ACB的旋转变换，生发出当旋转到特殊位置时探求旋转角度问题，应该说个角度还是好求的，我们可以用逆向思维来帮助思考．