2024年初中阶段三角形知识点汇总
 点击免费领取中考核心考点资料!
点击免费领取中考核心考点资料!
全等三角形
性质:
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
全等三角形的判定:
①边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等。
②角边角公理(ASA) 有两角和它们的夹边对应相等的两个三角形全等。
③推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等。
④边边边公理(SSS) 有三边对应相等的两个三角形全等。
⑤斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等。
方法总结:
出现两等边三角形、两等腰直角三角形通常用 SAS 证全等;
等腰直角三角形常见辅助线添法--连结直角顶点和斜边中点;
两直角三角形证全等常用方法:SAS,AAS,HL;出现等腰直角三角形或正方形可能用到 K 型全等。
角平分线
性质定理:
角平分线上的点到角两边的距离相等。
判定定理:
到角两个边距离相等的点在这个角的角平分线上。
拓展:三角形三个角的角平分线的交点到三条边的距离相等。
角平分线通常用于求点到直线距离、三角形面积角度。
拓展三个概念:
重心:
三角形中线的交点,重心分中线上下比为2:1。
内心:
三角形角平分线的交点,内心到三边的距离相等。
外心:
三角形垂直平分线的交点,外心到三个顶点的距离相等。
角平分线常见的四种辅助线做法:
①如下图,由角的平分线上的一点向角的一边或两边作垂线,可以用角的平分线性质定理解题;
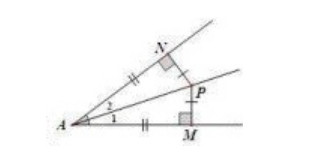
② 如下图,以角的平分线为轴,将图形翻折,在角的平分线两侧构造全等三角形,使已知与结论发生关系出现新的条件;

③ 如下图,当题设有角平分线及与角平分线垂直的线段,可延长这条线段与角的另一边相交,构成等腰三角形, 利用等腰三角形的“三线合一” 性质证题;
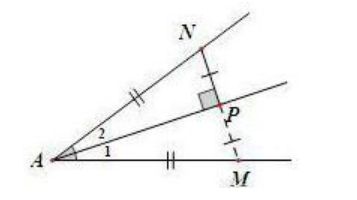
④如下图,过角的一边上的点,作另一边的平行线,构成等腰三角形——“角平分线+平行,必出等腰 ”
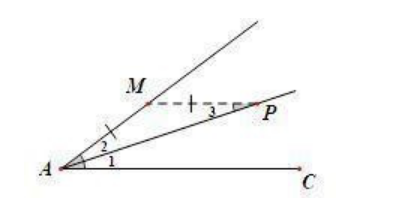
垂直平分线
性质定理:
线段垂直平分线上的点到线段两个端点的距离相等。
如何判定:
到线段两个端点距离相等的点在这条线段的垂直平分线上。
拓展:
三角形三条边的垂直平分线的交点到三个顶点的距离相等。
相关方法总结:
出现一点到两点距离相等的题型,一般要用到垂直平分线;
题中看到线段垂直平分线,要想到垂直平分线垂直且平分线段,垂直平分线上点到线段两端点距离相等,相等边所对应角相等;
翻折题型中常用到垂直平分线、勾股定理。
等腰三角形
性质定理:
等腰三角形的两个底角相等(等边对等角)
等腰三角形的顶角平分线、底边上的中线、底边上的高线互相重合(三线合一)
判断:一个三角形的两个相等的角所对的边也相等(等角对等边)
等边三角形
性质定理:
等边三角形的三条边都相等;
等边三角形的三个内角都相等,都等于60度。等边三角形的每一条边都能运用三线合一这一性质。
判断定理:
三条边都相等的三角形是等边三角形;
三个角都相等的三角形是等边三角形;
有两个角是 60°的三角形是等边三角形;
有一个角是 60°的等腰三角形是等边三角形。
方法总结:出现等腰三角形通常要分类讨论,在选择题和填空题中,切勿因为没有分类讨论而导致搞错答案。
直角三角形和勾股定理
有一个角是直角的三角形是直角三角形,在直角三角形中,斜边中线等于斜边的一半;
30度所对的直角边等于斜边的一半;直角三角形常用面积法求斜边上的高。
勾股定理:
直角三角形两直角边 a,b 的平方和等于斜边 c 的平方,即 a2+b2=c2。
勾股数一定是正整数,常见勾股数:
3,4,5;
5,12,13;
6,8,10,;
7,24,25;
8,15,17;
9,12,15。
方法总结:
当不明确直角三角形的斜边长,应把已知最长边分为直角边和斜边两种情况讨论。
无理数在数轴上的表示和线段长表示通常用到勾股定理。
翻折题型常用勾股定理(口诀:翻折求边找直角,勾股定理设未知量)
如果三角形的三边长 a,b,c 有关系 a2+b2=c2,那么这个三角形是直角三角形。勾股定理的逆定理,常用于判断三角形的形状,先确定最大边(可以设为c)

编辑推荐:




