三角形的角

内角

三角形三个内角的和等于180°.

因此推理可知，直角三角形的两个锐角互余;一个三角形中最多只有一个钝角或直角.

外角

三角形的外角和等于360°.

性质：

1.三角形的一个外角等于和它不相邻的两个内角的和

2.三角形的一个外角大于任何一个和他不相邻的内角

拓展：多边形的角

内角：

n边形的内角和为：(n-2)x180°(n≥3)，正n边形每个内角的度数为：(n-2)x180°÷n.

外角：

多边形的外角和为360°;正多边形的每个外角和度数为360°÷n.

三角形的

三线

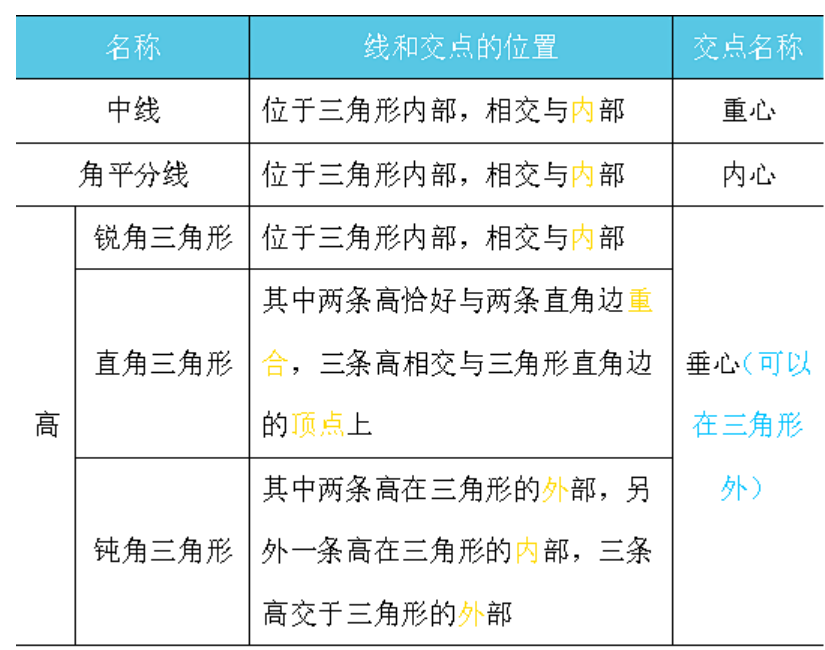
高：从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高.三角形的高的垂足不一定落在三角形的边上，有可能落在边的延长线上.

中线：在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线.

角平分线：三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线

特殊

的三角形

等腰三角形

有两条边相等的三角形叫做等腰三角形相，等的两条边叫做腰，另一条边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫底角.

等腰三角形的性质：

1.等腰三角形的两个底角相等.(等边对等角)

2.等腰三角形的顶角平分线，底边上的中线底边上的高相互重合.

3.等腰直角三角形的两个底角相等，且等于45°.

判定方法：

1.有两条边相等的三角形叫做等腰三角形.

2.如果一个三角形的两个角相等，那么这两个角所对的边也相等，及这个三角形为等腰三角形.(等角对等边)

对于等腰三角形的问题，我们在说角或边时一般都要指明是顶角还是底角，是底边还是腰?若是没有说明，则两者都有可能需要分类讨论，这是解决等腰三角形问题，最容易忽视和产生错误的地方.

等边三角形

三条边都相等的三角形叫做等边三角形，也叫正三角形.等边三角形的内心，外心，重心和垂心四心合一.

性质：

1.等边三角形的三个内角都相等，并且每一个角都等于60°.

2.等边三角形是轴对称图形，它有三条对称轴，三条对称轴相交于一点，该点称为中心.

3.等边三角形是特殊的等腰三角形，它具有等腰三角形的一切性质,等边三角形每条边上的中线、高和所对角的平分线“三线合一”.

判定方法：

1.三条边都相等的三角形是等边三角形.

2.三个角都是相等的，三角形是等边三角形.

3.有一个角是60°的等腰三角形是等边三角形.

含30°角的直角三角形

在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半

全等

三角形

能够完全重合的两个三角形叫做全等三角形.

全等符号用全等用符号“≌”表示，读作：“全等于”，△ABC≌△A'B'C'读作“三角形ABC全等于三角形A'B'C' ”.

全等三角形的性质

1.全等三角形的对应边相等，对应角相等.

2.全等三角形的周长相等面积相等.

3.全等三角形的对应边上的对应中线，角平分线，高线分别相等.

三全等三角形的判定定理

1. SSS(边边边)

三边分别相等的两个三角形全等.

2. SAS(边角边)

两边和它们的夹角分别相等的两个三角形全等.

3. ASA(角边角)

两角和它们的夹边分别相等的两个三角形全等.

4. AAS(角角边)

两角和其中一角的对边分别相等的两个三角形全等.。

5. HL(斜边、直角边)

斜边和一条直角边分别相等的两个直角三角形全等.

三角形全等的判定方法的选择

相似

三角形

性质

1. 相似三角形对应线段的比等于相似比

相似三角形的对应角相等，对应边成比例，且对应边的比对应高的比，对应中线的比与对应角平分线的比都等于相似比.

2. 相似三角形面积的比等于相似比的平方

相似三角形周长的比等于相似比，面积的比等于相似比的平方.

判定

1.预备定理：平行于三角形一边的直线和其他两边相交所构成的三角形与原三角形相似.

2.判定定理一：三边对应成比例的两个三角形相似.

3.判定定理二：两边对应成比例且夹角相等的两个三角形相似.

4.判定定理三：两角分别相等的两个三角形相似.

5.直角三角形相似的判定定理：一个锐角相等的两个直角三角形相似.

两组直角边成比例的两个直角三角形相似.

斜边和一条直角边成比例的两个直角三角形相似.

应用

此类题答题的核心就是要构造相似三角形。

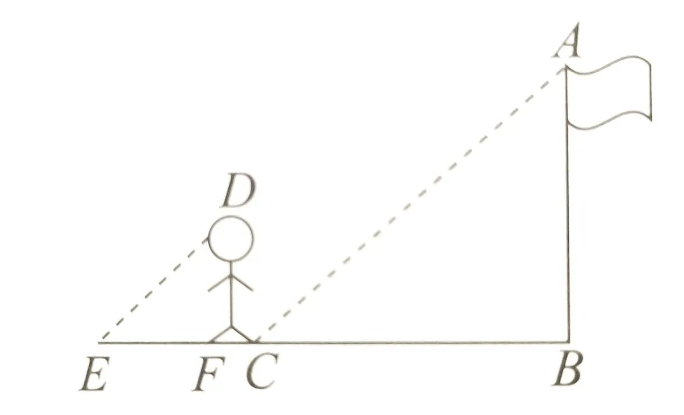
1.利用阳光下的影子测量物体的高度

条件：参照物的高度，参照物的影长，被测物体的影长.

原理：是同一时刻，同一地点，物高与影长成比例.

公式：AB= DF/FE·BC

2.利用灯光下的影子测量路灯的高度。

条件：人的身高，人的影子长，影子顶端到路灯底部的距离.

原理：人的身高，路灯的高度，人的影子长，影子顶端到路灯底部的距离成比例.

公式：AB=CD/DE ·BE

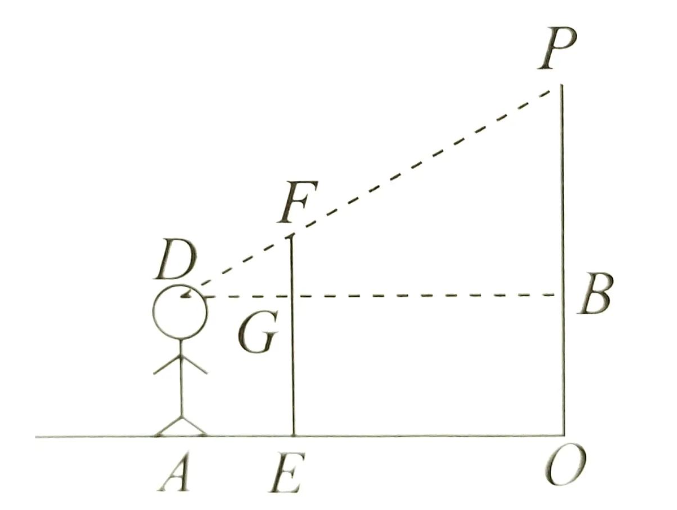
3.利用标杆测量物体的高度

条件：人的身高，人到物体的距离，人到标杆的距离，标杆的高度.

原理：构造相似三角形，把被测物体分成两部分求解.

公式：PB=BD/GD ·FG，PO=PB+AD

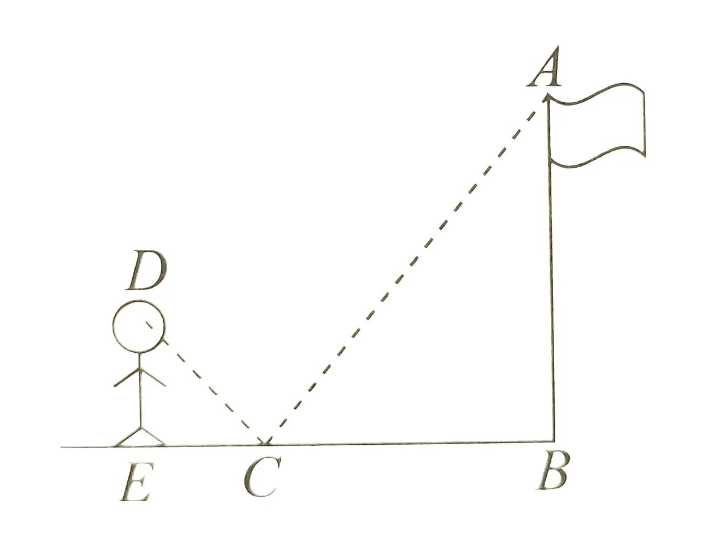
4.利用镜子的反射测量物体的高度

条件：人的身高，人到镜子的距离，物体到镜子的距离.

原理：根据入射角等于反射角构造相似三角形.

公式：AB=DE/EC ·BC

       编辑推荐：

       2024年中考各科目重点知识汇总