一、二次函数相关考试题型

二次函数的考试题型主要包括，二次函数的图像与性质，二次函数的解析式，二次函数的对称轴，二次函数的顶点坐标，还有二次函数的的平移或者对折，根据y的取值找x的取值范围，或者根据x的取值找y的取值范围，二次函数和一元二次方程的关系等。

二次函数经常以压轴题的形式出现，有些是和一元二次方程结合在一起的，有些是和几何结合在一起的，难度各有不同。

二、初中二次函数有哪些题型

回答一：和几何结合

和几何结合在一起，可以是动点求最短线段，这是最简单的;也可以是和三角形，四边形相结合。

较复杂的是二次函数和四边形还有和动圆相结合的综合性题目。但是，现在的中考数学，二次函数和圆综合的压轴题越来越少了，一般都是和三角形，四边形，动点结合。但是和圆结合的题，同学们也要把历年的中考真题认真做懂做透。

回答二：点存在性问题

二次函数图象上的点存在性问题。

知识点：二次函数的基本性质、待定系数法求函数解析式、图形的旋转、抛物线与直线相交(二次函数与一次函数)、确定二次函数的条件。

三、典例详解

【题目】

抛物线C1：y=2x2+mx+m过定点M，其顶点P的坐标为(p，q)，将点M绕原点逆时针旋转90°得到点N，抛物线C2：y=ax2+bx+c经过点M，N。

(1)填空：M(_____，_____)，N(_____，_____);

(2)用含p的代数式表示q;

(3)当抛物线C1与线段OM恰有两个交点时，试确定m的取值范围;

(4)若无论a，b，c取何值，抛物线C2都不经过点P，请求出点P的坐标。

【解析】

(1)将抛物线C1的解析式变换成y=2x2+m(x+1)后观察，既然是过定点M，则无论m取何值，解析式两边恒成立，于是令x=-1，使含m的项为零，从而得到y=2，于是可知定点M的坐标为(-1，2)，由旋转可得N(-2，-1);

(2)直接利用二次函数顶点坐标公式：

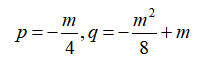
将前一个式子变换为m=-4p，代入第二个式子即可得到q=-2p2-4p;

(3)抛物线与线段有两个交点，前提是与线段所在直线有两个交点，直线OM解析式为y=-2x，联立抛物线与直线方程：-2x=2x2+mx+m，整理成(2x+m)(x+1)=0，于是解出x1=-m/2，x2=-1，其中x2其实就是点M的横坐标，那么另一个交点横坐标必须在-1和0之间，才能保证抛物线与线段有两个交点，于是列出不等式，解得。

(4)本题难点，抛物线不经过点P，根据平面直角坐标系内确定抛物线的条件，至少三个不同的点，且满足①不在同一直线上;②没有任意两点横坐标相同。由抛物线C2：y=ax2+bx+c经过点 M(-1，2)和点N(-2，-1)，可得抛物线C2的解析式为y=ax2+(3a+3)x+2a+5，若P在抛物线C2上，则-2p2-4p=ap2+(3a+3)p+2a+5，即(p+1)[(a+2)p+2a+5]=0，当 p=-1时，P(-1，2)即是定点M在抛物线C2上，由(a+2)p+2a+5=0得(p+2)a=-5-2p，当p+2=0时，(p+2)a=-5-2p无解，此时P(-2，0)，当-5-2p=0时，因a≠0，故(p+2)a=-5-2a无解，此时P(-5/2，-5/2)，故抛物线C2：y=ax2+(3a+3)x+2a+5总不经过P(-2，0)和(-5/2，-5/2)。

       编辑推荐：

       2023年中考各科目重点知识汇总