1.修路问题

例题1：如图，在宽为20m，长为30m的矩形地面上修建两条同样宽且互相垂直的道路，余下部分作为耕地面积为551m2。则道路的宽是多少米?

分析：本题主要考查了一元二次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解。

解法1：要求修建的路宽，就设修建的路宽应为x米，根据题意可知，矩形的面积-所修路的面积=耕地面积，依此列出等量关系解方程即可。

解：设修建的路宽应为x米。

根据等量关系列方程得，30×20-(20x+30x-x2)=551

整理可得x2-50x+49=0，

解得x1=1，x2=49>20(不符合题意，舍去)。

答：道路的宽为1米。

解法2：将两条路全部移到旁边，耕地就变成了一个矩形，利用矩形的面积计算即可。

解：设修建的路宽应为x米。

(20-x)(30-x)=551，

解得x1=1，x2=49>20(不符合题意，舍去)。

答：道路的宽为1米。

2.养鸡场围篱笆问题

例题2：如图某农场要建一个长方形的养鸡场，鸡场的一边靠墙(墙长18m)，另三边用木栏围成，木栏长35m。鸡场的面积能达到180m2吗?如果能，请你给出设计方案;如果不能，请说明理由。

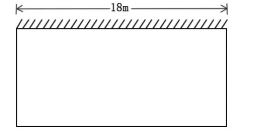
分析：可设垂直于墙的一边长x米，得到平行于墙的一边的长，根据面积为150列式求解，并使平行于墙的一边的长小于18即可。

解：设与墙垂直的一边长为x m，则与墙平行的一边长为(35-2x)m。

根据题意可列方程为x(35-2x)=150，

整理得2x2-35x+150=0，

解得x1=10，x2=7.5。

当x=10时，35-2x=15;

当x=7.5时，35-2x=20>18(舍去)。

答：鸡场的面积能达到150m2，方案是与墙垂直的一边长为10m，与墙平行的一边长为15m。

       编辑推荐：

       2023年中考各科目重点知识汇总