知识回顾

平面直角坐标系中一个点 P(m，n)

①若向上平移t(t>0)个单位，向y轴正半轴方向平移，横坐标值不变，纵坐标值变大。平移后的点P1(m，n+t);

②若向下平移t(t>0)个单位，向y轴负半轴方向平移，横坐标值不变，纵坐标值变笑。平移后的点P2(m，n-t);

③若向右平移t(t>0)个单位，向x轴正半轴方向平移，纵坐标值不变，横坐标值变大。平移后的点P3(m+t，n);

④若向左平移t(t>0)个单位，向x轴负半轴方向平移，纵坐标值不变，横坐标值变小。平移后的点P3(m-t，n)

口诀：“上加下减、左减右加”

例题讲解

例1：点(2，3)向下平移2个单位再向右平移3个单位，则坐标变为(　D　)

A.(4，6)B.(0，0)C.(0，6)D.(5，1)

解：原来点的横坐标是2，纵坐标是3，向下平移2个单位再向右平移3个单位，

得到新点的横坐标是2+3=5，纵坐标为3﹣2=1.即坐标变为(5，1).

例2：由点A(﹣5，3)到点B(3，﹣5)可以看作(　C　)平移得到的.

A.先向右平移8个单位，再向上平移8个单位

B.先向左平移8个单位，再向下平移8个单位

C.先向右平移8个单位，再向下平移8个单位

D.先向左平移2个单位，再向上平移2个单位

解：从点A(﹣5，3)到点B(3，﹣5)，横坐标+8，纵坐标﹣8，故先向右平移8个单位，再向下平移8个单位。

图形的平移

知识回顾

①图形平移前后形状不变，图形上的点的相对位置也不改变，只有图形所在的位置改变;

②图形上每个点平移的路径是完全一样的(“平行”且相等);

③平移中，对应点的对应坐标的变化相同，对应坐标的差相等

例题讲解

例3：线段CD是由线段AB平移得到的.点A(﹣1，4)的对应点为C(4，7)，则点B(﹣4，﹣1)的对应点D的坐标为(　C　)

A.(2，9) B.(5，3)

C.(1，2) D.(﹣9，﹣4)

解：平移中，对应点的对应坐标的差相等，设D的坐标为(x，y);根据题意：有4﹣(﹣1)=x﹣(﹣4);7﹣4=y﹣(﹣1)，解可得：x=1，y=2;故D的坐标为(1，2).

例4：△DEF(三角形)是由△ABC平移得到的，点A(﹣1，﹣4)的对应点为D(1，﹣1)，则点B(1，1)的对应点E，点C(﹣1，4)的对应点F的坐标分别为(　B　)

A.(2，2)，(3，4)

B.(3，4)，(1，7)

C.(﹣2，2)，(1，7)

D.(3，4)，(2，﹣2)

解：点A的对应点D，是横坐标从﹣1到1，说明是向右移动了1﹣(﹣1)=2个单位，纵坐标是从﹣4到﹣1，说明是向上移动了﹣1﹣(﹣4)=3个单位，那么其余两点移运转规律也如此，即横坐标都加2，纵坐标都加3.故点E、F的坐标为(3，4)、(1，7).故选B.

函数图象的平移

知识回顾

先回顾下两直线平移：

若直线y1=k1x+b1与直线y2=k2x+b2平行，那么k1=k2，且b1≠b2

(若k1=k2，且b1=b2，则这两条直线重合)

知识拓展：斜着平移

二次函数图象的斜着平移

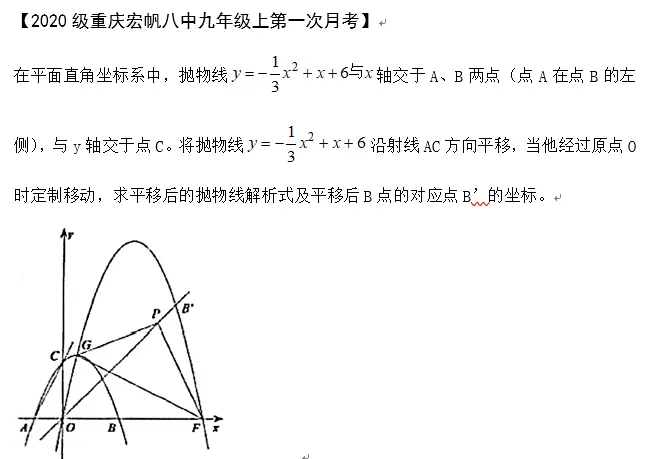
二次函数图象的斜着平移在19年重庆中考B卷26题第二问中出现过，最近八中的月考也出现了，如果第一次见到会比较慌张，不知道如何下手，实际上把这个单独拿出来看，就是一个简单的平移问题，用函数图象平移打方法处理就可以了。

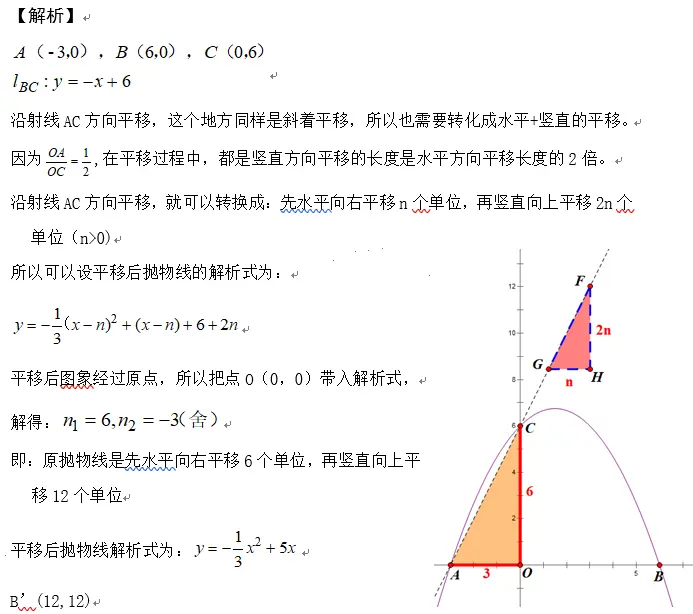
【小结】初中阶段，平面直角坐标系中的平移问题就这么多，简单的就是水平和竖直方向的平移，但是要把点和函数的平移区分开。

斜着平移就转换成水平+竖直方向的平移，要相信，斜着的平移是一定能转换成“水平+竖直”的平移的!!!

       编辑推荐：

       2023年中考各科目重点知识汇总