下面，将分类进行探讨：

一、求点关于点的对称点坐标；

二、求点关于坐标轴（或平行于坐标轴）的对称点坐标；

三、求点关于一次函数的对称点坐标。

一、点关于点的对称

实质：该点是两对称点连线段的中点。

中点坐标公式

方法：利用。

说明：

(1)点P(a,b)关于点A(x,y)的对称点的坐标为P’(2x-a,2y-b);

x、y均互为相反数。

(2)点P(a,b) 关于原点O(0,0)的对称点P’(-a,-b)，特点为：

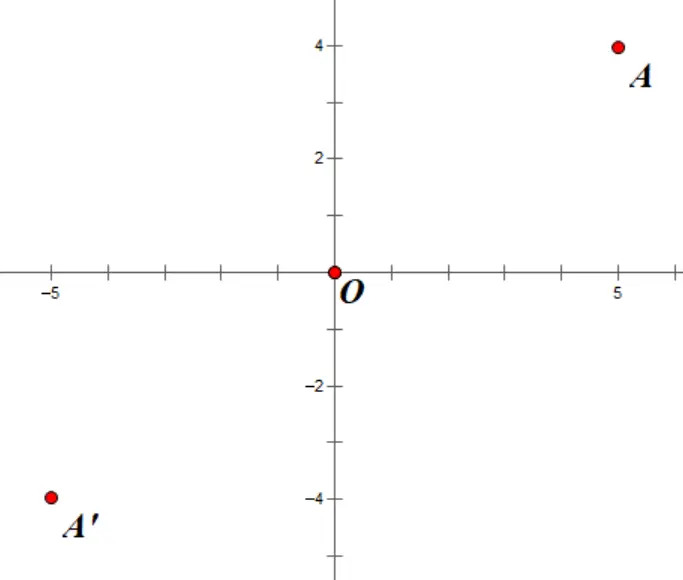
二、点关于坐标轴（平行于坐标轴）对称

实质：轴(直线)是对称点连线段的中垂线

(一)关于x轴对称

1.关于x轴对称

x不变，y互为相反数

一个点A(a,b)关于x轴对称的点的坐标为A’(a,-b)，特点为：。

2.关于平行于x轴的直线对称

x不变，y相加等于2m

一个点A(a,b)关于直线y=m对称的点的坐标为A’(a,2m-b)，特点为：。

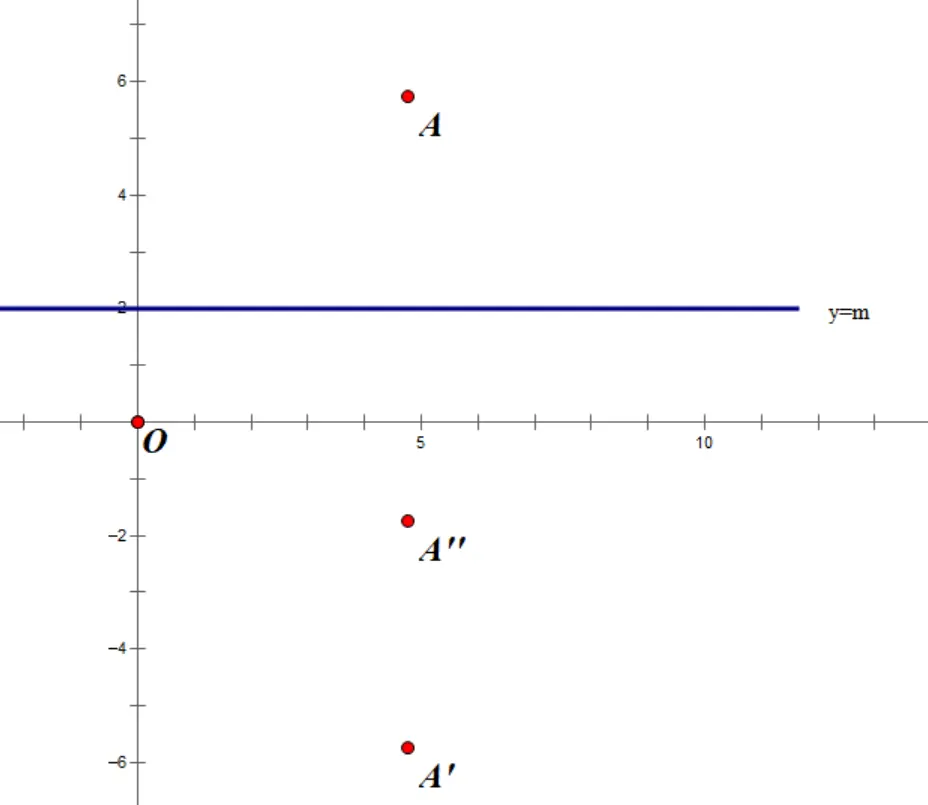
例：A(-3,5)关于x轴对称的点的坐标为A’(____,____).

解：点A、A’关于x轴对称

∴横坐标不变，纵坐标互为相反数

∴A’(-3，-5)

例：A(-3,5)关于直线y=1对称的点的坐标为A’(____,____).

解：点A、A’关于直线y=1对称

∴横坐标不变，纵坐标相加等于2

∴A’(-3，-3)

(二)关于y轴对称

1.关于y轴对称

y不变，x互为相反数

一个点A(a,b)关于y轴对称的点的坐标为A’(-a,b)，特点为：。

2.关于平行于y轴的直线对称

y不变，x相加等于2m

一个点A(a,b)关于直线x=m对称的点的坐标为A’(2m-a,b)，特点为：。

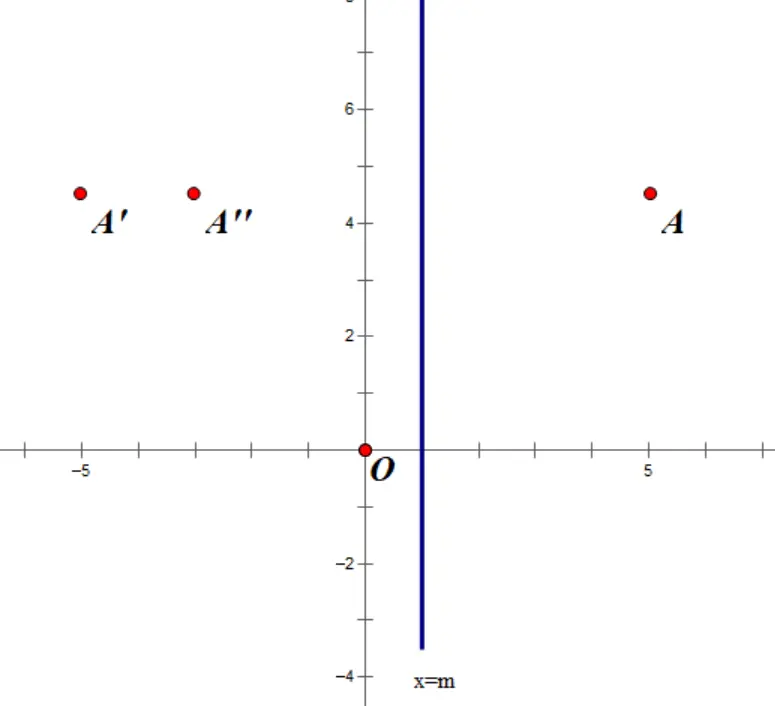
例：A(-3,5)关于y轴对称的点的坐标为A’(____,____).

解：点A、A’关于y轴对称

∴纵坐标不变，横坐标互为相反数

∴A’(3，5)

例：A(-3,5)关于x=1对称的点的坐标为A’(____,____).

解：点A、A’关于直线x=1对称

∴纵坐标不变，横坐标相加等于2

∴A’(5，-3)

三、关于一次函数y=kx+b对称

已知点A坐标与直线解析式，求点A关于直线对称的点A’的坐标。

1.解析式法

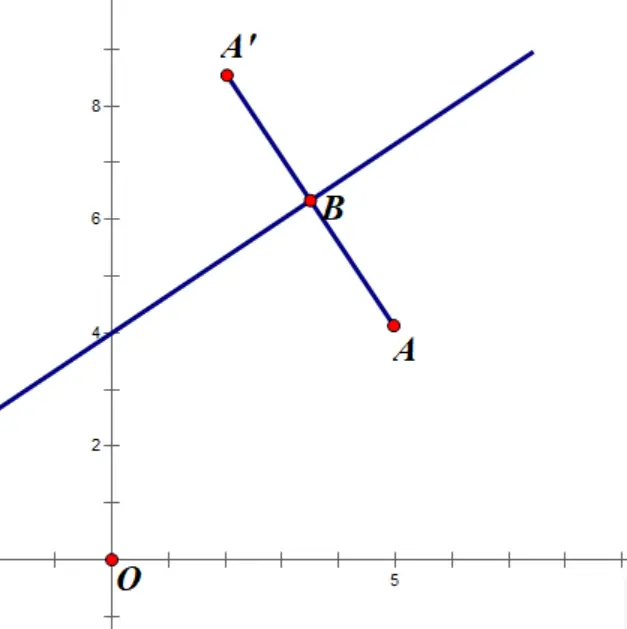
(1)两直线垂直，k1·k2=-1

(2)AA'的解析式

(3)点B的坐标

(4)利用中点坐标公式

2.几何法（化斜为直）

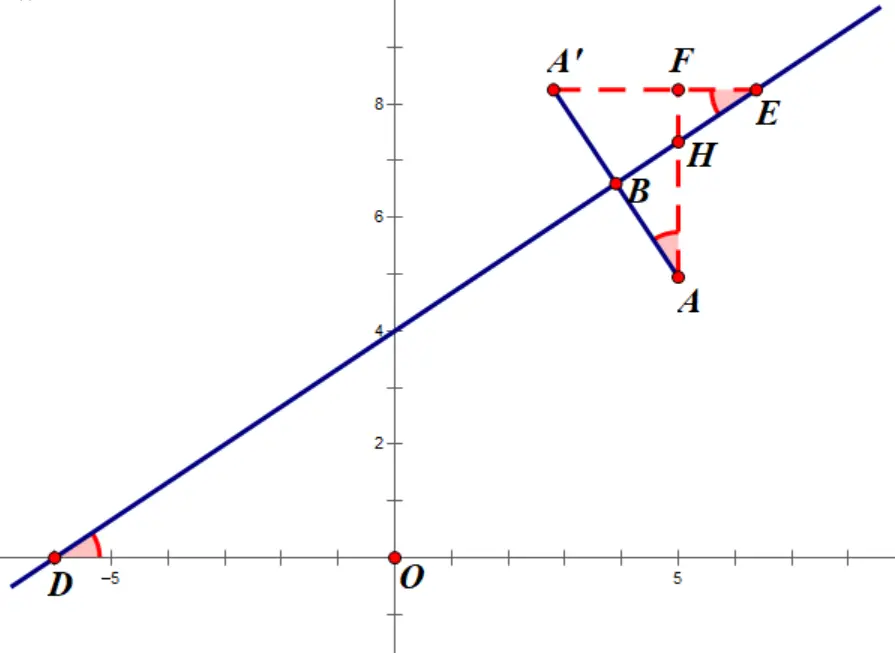
(1)求出点H的坐标，可得AH的长度

(3) 求AB的长度(三角函数)

(4) AA'=2AB

(5) 求AF、A'F的长度(三角函数)

(6)可得点A’的坐标

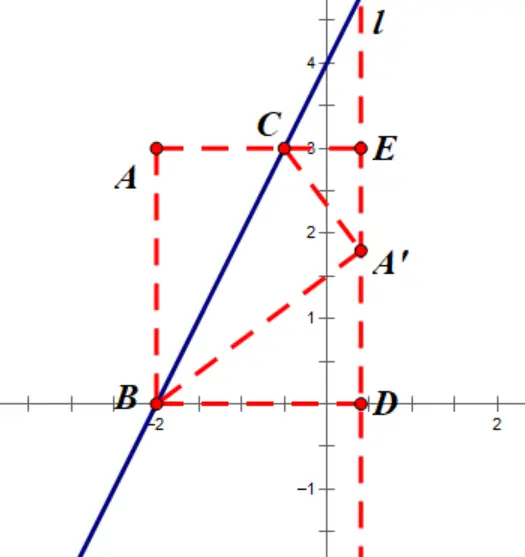
3 .几何法（构造“K字形”相似）

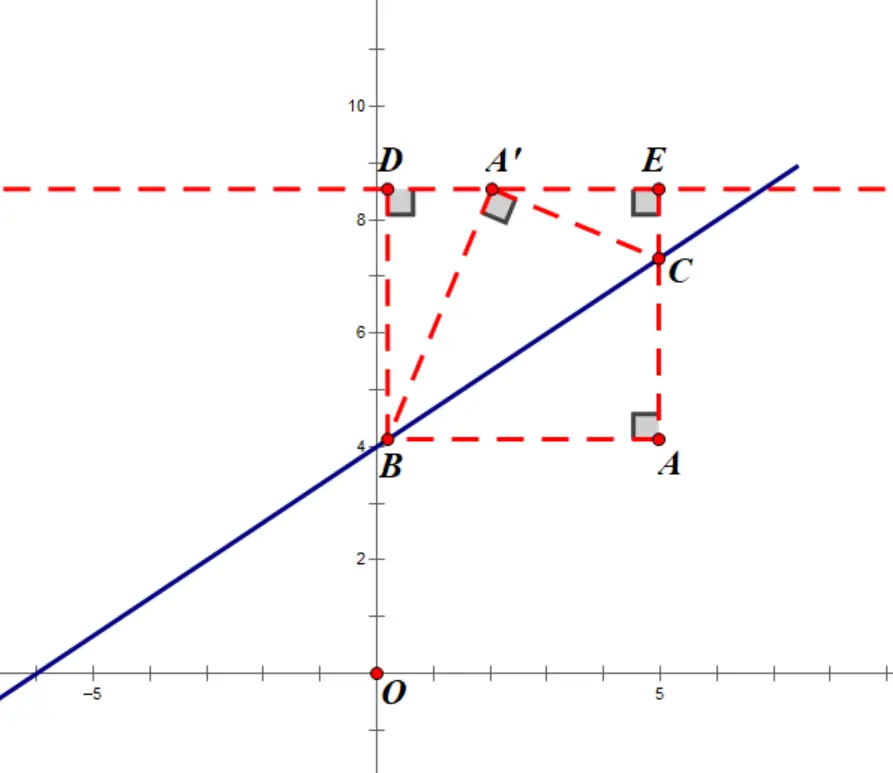
(1)过点A作x轴、y轴的平行线，分别交直线点B、C，连接A’B、A’C(△ABC≌△A’BC)

(2)过点A’作x轴的平行线，过点B、C作这条线的垂线交于点D、E(构造“K字形”相似)

(3)可求AC、AB的长

(4)

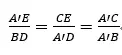
(5)可得点A’的坐标

【例】如图，在平面直角坐标系中，已知点A(-2,3)关于一次函数y=2x+4的对称点为A’，求点A’的坐标。

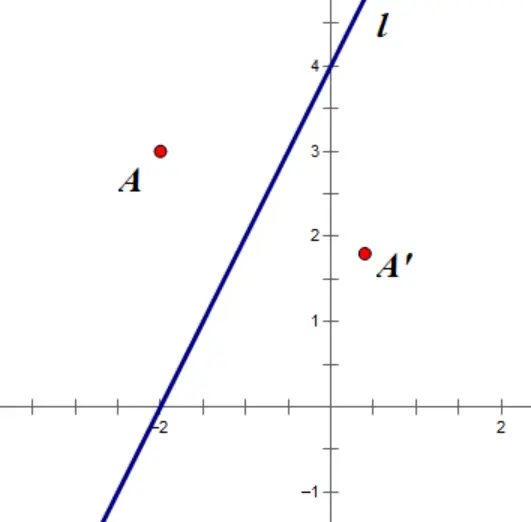
解法一：解析式法

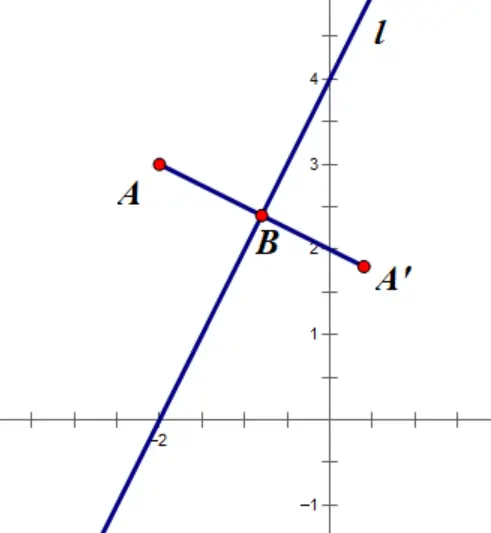
解法二：几何法（化斜为直）

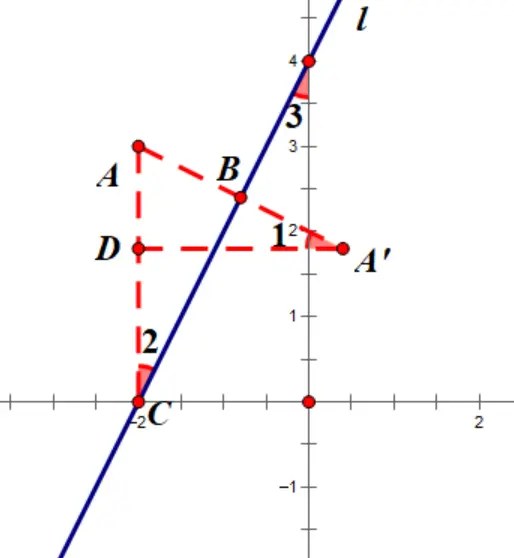
解法二：几何法（构造“K字形”相似）

       编辑推荐：

       2023年中考各科目重点知识汇总