一、圆的有关概念

1.与圆有关的概念和性质

1)圆：平面上到定点的距离等于定长的所有点组成的图形.

2)弦与直径：连接圆上任意两点的线段叫做弦，过圆心的弦叫做直径，直径是圆内最长的弦.

3)弧：圆上任意两点间的部分叫做弧，小于半圆的弧叫做劣弧，大于半圆的弧叫做优弧.

4)圆心角：顶点在圆心的角叫做圆心角.

5)圆周角：顶点在圆上，并且两边都与圆还有一个交点的角叫做圆周角.

6)弦心距：圆心到弦的距离.

2.注意

1)经过圆心的直线是该圆的对称轴，故圆的对称轴有无数条;

2)3点确定一个圆，经过1点或2点的圆有无数个.

3)任意三角形的三个顶点确定一个圆，即该三角形的外接圆.

二、垂径定理及其推论

1.垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.

关于垂径定理的计算常与勾股定理相结合，解题时往往需要添加辅助线，一般过圆心作弦的垂线，构造直角三角形.

2.推论

1)平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧;

2)弦的垂直平分线经过圆心，并且平分弦所对的两条弧.

三、圆心角、弧、弦的关系

1.定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等.圆心角、弧和弦之间的等量关系必须在同圆等式中才成立.

2.推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等.

四、圆周角定理及其推论

1.定理：一条弧所对的圆周角等于它所对的圆心角的一半.

2.推论：1)在同圆或等圆中，同弧或等弧所对的圆周角相等. 2)直径所对的圆周角是直角.

圆内接四边形的对角互补.在圆中求角度时，通常需要通过一些圆的性质进行转化.比如圆心角与圆周角间的转化;同弧或等弧的圆周角间的转化;连直径，得到直角三角形，通过两锐角互余进行转化等.

五、与圆有关的位置关系

1.点与圆的位置关系

设点到圆心的距离为d.

(1)d

(2)d=r⇔点在⊙O上;

(3)d>r⇔点在⊙O外.

判断点与圆之间的位置关系，将该点的圆心距与半径作比较即可.

2.直线和圆的位置关系

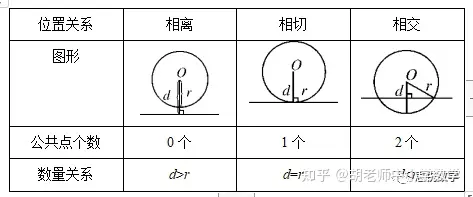
由于圆是轴对称和中心对称图形，所以关于圆的位置或计算题中常常出现分类讨论多解的情况.

六、切线的性质与判定

1.切线的性质

1)切线与圆只有一个公共点.2)切线到圆心的距离等于圆的半径.3)切线垂直于经过切点的半径.

利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题.

2.切线的判定

1)与圆只有一个公共点的直线是圆的切线(定义法).

2)到圆心的距离等于半径的直线是圆的切线.

3)经过半径外端点并且垂直于这条半径的直线是圆的切线.

切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直;②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径.

七、三角形与圆

1.三角形的外接圆相关概念

经过三角形各顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形.外心是三角形三条垂直平分线的交点，它到三角形的三个顶点的距离相等.

2.三角形的内切圆

与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形.内心是三角形三条角平分线的交点，它到三角形的三条边的距离相等.

八、正多边形的有关概念

正多边形中心：正多边形的外接圆的圆心叫做这个正多边形的中心.

正多边形半径：正多边形外接圆的半径叫做正多边形半径.

正多边形中心角：正多边形每一边所对的圆心角叫做正多边形中心角.

正多边形边心距：正多边形中心到正多边形的一边的距离叫做正多边形的边心距.

九、与圆有关的计算公式

1.弧长和扇形面积的计算：

扇形的弧长;

扇形的面积.

2.圆锥与侧面展开图

1)圆锥侧面展开图是一个扇形，扇形的半径等于圆锥的母线，扇形的弧长等于圆锥的底面周长.

2)若圆锥的底面半径为r，母线长为l，则这个扇形的半径为l，扇形的弧长为2πr，

圆锥的侧面积为S圆锥侧=.

圆锥的表面积：S圆锥表=S圆锥侧+S圆锥底=πrl+πr2=πr·(l+r).

在求不规则图形的面积时，注意利用割补法与等积变化方法归为规则图形，再利用规则图形的公式求解.

在中考中一般会在解答题位置考查到圆的综合题，涉及到圆的相关证明和计算，这类题目不仅仅会考查到圆的相关知识点，还会涉及到平行线、等腰三角形、直角三角形、全等三角形、相似三角形、三角函数、特殊四边形等知识点，有一定的综合性。

       编辑推荐：

       2023年中考各科目重点知识汇总