两圆一线

一线，指的是线段的中垂线;

两圆，指的是以线段长度为半径，线段端点为圆心而产生的两个圆。

首先，我们来解决第一个问题，等腰三角形的生成问题。

在平面内有一线段AB，点C为平面内任意一点，若△ABC为等腰三角形，则这样的点C有几个?点C的轨迹又是什么?根据等腰三角形的性质，线段AB有可能为底边，也有可能为腰，故有两种基本情况。：线段AB为底边，则有AC=BC，即点C到线段AB两端点的距离相等，故点C在线段AB的中垂线上，此时点C有无数个，点C的轨迹为直线(不取与AB相交的点)，如下图：

情况（2）

：线段AB为腰，则有：①AB=AC，即点C到点A的距离等于点B到点A的距离，则点C在以点A为圆心，AB长为半径的圆上，此时点C有无数个，点C的轨迹为圆(不取点B和与A、B共线点)，如下图：②AB=BC，即点C到点B的距离等于点A到点B的距离，则点C在以点B为圆心，AB长为半径的圆上，此时点C有无数个，点C的轨迹为圆(不取点A和与A、B共线的点)，如下图：

请记住这两圆一线：

综上所述，这样的点C有无数个，点C的轨迹为两个圆和一条直线，为了方便记忆，我们简称“两圆一线”，这是等腰三角形存在性处理的基本定性策略。

- 嘉成老师解析 -

同学们～碰到一次函数跟几何结合的题目，等腰三角形的存在性问题时，要想到两圆一线的方法;每一个点都有可能是定点，所有分3种情况进行讨论，其中一种是找垂直平分线，另外两种是以给定的一个点为圆心，线段长度为半径，垂直平分线/圆与所给线段的交点，即为所求。

其次，我们来解决第二个问题，等腰三角形的边长问题。

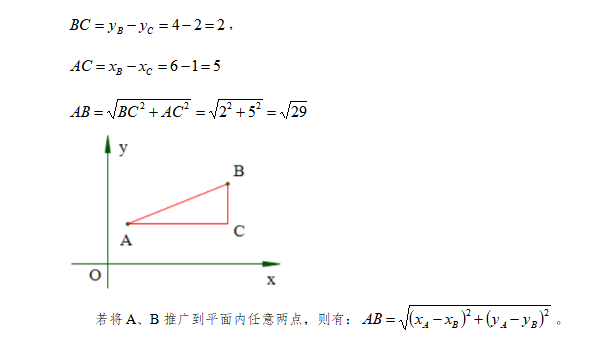
求等腰三角形的边长，我们通常将其转化为两点间的距离问题，所以，我们来推导一下平面内两点间的距离公式。已知平面内两点A(1,2)、B(6,4)，求线段AB的长度。连接AB，以AB为斜边，构造直角边与坐标轴平行的直角三角形，利用勾股定理解题，如下图：

     编辑推荐：

      2023年中考各科目重点知识汇总