一次函数的基本内容

兵马未动，粮草先行。认识一次函数，首先得从基础抓起，概念理解不透彻，知识掌握不牢固，做起题目来必然也会磕磕碰碰，不得其解。

1、表达式：

一般地，形如y=kx+b(k，b是常数，k≠0)，那么y叫做x的一次函数。

(当b=0时，y=kx+b即y=kx，所以说正比例函数是一种特殊的一次函数)

一次函数一般形式 y=kx+b成立的条件：

● k不为零

● x指数为1

● b取任意实数

2、函数图象：

(1)一次函数y=kx+b的图象是经过(0，b)和(-b/k，0)两点的一条直线，我们称为直线y=kx+b，它可以看作由直线y=kx平移|b|个单位长度得到。

(2)走向：k>0，图象经过第一、三象限;k<0，图象经过第二、四象限;b>0，图象经过第一、二象限;b<0，图象经过第三、四象限。

3、增减性：

k>0，y随x的增大而增大;k<0，y随x增大而减小。

总结：

(1)k>0且b>0 直线经过第一、二、三象限，y随x的增大而增大。

(2)k>0且b<0 直线经过第一、三、四象限，y随x的增大而增大。

(3)k<0且b>0 直线经过第一、二、四象限，y随x的增大而减小。

(4)k<0且b<0直线经过第二、三、四象限，y随x的增大而减小。

4、图像的平移：

遵循“上加下减，左加右减”的原则：

当b>0时，将直线y=kx的图象向上平移b个单位;

当b<0时，将直线y=kx的图象向下平移b个单位。

5、一次函数的对称

若两函数关于x轴对称，则y=kx+b变成y=-kx-b，交点为(-b/k，0);

若两函数关于y轴对称，则y=kx+b变成y=-kx+b，交点为(0，b);

若两函数关于x=n对称，则y=kx+b变成y=-kx+2nk+b，交点为(n，kn+b);

若两函数关于y=n对称，则y=kx+b变成y=-kx+(2n-b)，交点为[(n-b)/k，n];

若两函数关于原点对称，则y=kx+b变成y=kx-b，无交点。

一次函数的应用

一次函数的应用题，信息量大，综合性强，不仅仅考察了一次函数的图像及性质，还考察了阅读理解能力及构造方程的能力等，对于初学者来说，无疑是一个难点。一、一次函数图象的基本应用

我们需要知道：任何一元一次方程到可以转化为ax+b=0(a，b为常数，a≠0)的形式，所以解一元一次方程可以转化为：当某个一次函数的值为0时，求相应的自变量的值。从图象上看，相当于已知直线y=ax+b确定它与x轴的交点的横坐标的值。

当需要利用函数和函数图象比较数的大小，主要有三种方法：

(1)直接把x值代入函数关系式，求出相应的y值，比较数的大小;

(2)在函数图象上描出各点，再根据各点的位置情况，比较数的大小;

(3)利用函数的增减性，比较数的大小。

涉及一次函数的图像的相关题目，需要充分运用数形结合的思想，对其单调性、经过的象限，交点等知识点进行考察，这类题目的难易程度一般，基本在选择题和填空题出现。

二、待定系数法求函数解析式

确定函数解析式的一般步骤：

(1)根据已知条件写出含有待定系数的函数关系式;

(2)将x、y的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程;

(3)解方程得出未知系数的值;

(4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式。

三、一次函数的综合考察

在初中的数学学习中，一次函数与反比例函数、二次函数相结合的题目出现较多，这些题型综合考查一次函数、反比例函数、二次函数等的知识，还能够与其他知识结合起来。解题时，涉及交点时要注意充分应用交点在两个函数的图象上的条件。

例如：涉及一次函数与一元一次不等式的知识点，可以将一元一次不等式转化为ax+b>0或ax+b<0(a，b为常数，a≠0)的形式，所以解一元一次不等式可以看作：当一次函数值大(小)于0时，求自变量的取值范围。

课堂总结

1、解决一次函数应用问题的步骤：

◆分析问题：

(1)借助图、表等手段分析题目中的数量关系，从而确定函数解析式;

(2)根据函数图像获取信息，分析数量关系。

◆确定模型：根据获取到的信息确定一次函数模型。

◆解决问题：根据题目中的数量关系或者数学模型，将具体数字代入，从而解决问题。

2、注意事项：■ 对于有图象的应用题，首先从函数的图像入手，搞清楚函数图像的实际意义，把那些关键的点，线给求出来，往往能够起到事半功倍的效果。

■ 搞定了图象，再看题目的关键信息，许多问题就迎刃而解。

■ 对于没有图象的应用题，一边读题，一边将关键的数据及数据之间的关系罗列出来——通过读题把文字语言翻译成数学语言。

课后练习

已知A、B两地之间的笔直公路上有一处加油站C(靠近B地)，一辆客车和一辆货车分别从A、B两地出发，朝另一地前进，两车同时出发，匀速行驶.如图所示是客车、货车离加油站C的距离y₁，y₂(千米)与行驶时间x(小时)之间的函数关系图像。

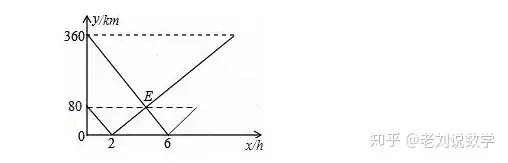
(1)求客车和货车的速度;

(2)图中点E代表的实际意义是什么，求点E的横坐标。