203年初中数学基础知识:整式
 点击免费领取中考核心考点资料!
点击免费领取中考核心考点资料!
整式
考点一:整式
单项式与多项式统称为整式(注意前一章的代数式的分类,观察两者之间的关系)
注意:1.所有整式的分母中不含字母
2.所有的整式都是代数式,但并不是所有的代数式都是整式
考点二:单项式
1. 像-x、-ab、2πr,都是数与字母的积,这样的式子叫做单项式.单独的一个数或者一个字母也是单项式
注意:1.单项式的记忆方法“只含乘法,不含加减法”。
2.由于π是常数,所以1/π也是常数,是单项式
2.单项式的系数:单项式中的数字因数叫做这个单项式的系数,如:2x的系数是2、 -abc的系数是-1
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数
考点三:多项式
1. 多项式:(1)几个单项式的和叫做多项式,(2)在多项式中,每个单项式叫做多项式的项。(3)在多项式中,不含字母的项叫做常数项
注意:1.多项式的每一项都包括它前面的符号
2.多项式中单项式的个数叫做多项式的项数,如3a-2a+5的项数是三,叫做3项式
2.多项式的次数:在一个多项式中,次数最高项的次数,叫做这个多项式的次数;多项式经常以它的次数和项数来命名,称几次几项式;如:6xy4+2x2y2-3xy-4就是五次四项式
4.2整式的加减法
考点一:同类项
1. 所含字母相同,并且相同字母的指数也分别相同的项叫做同类项;如-5a和3a是同类项, -4和5也是同类项
2. 判别同类项的标准有两个:(1)所含字母相同 (2)相同字母的指数也分别相同, 两者缺一不可
3. 同类项与系数无关,与字母的排列顺序无关
考点二:合并同类项
把同类项的系数相加,所得结果作为合并后的系数,字母和字母的指数保持不变
考点三:整式的加减
1. 去括号法则:
(1)括号前面是“+”号,把括号和它前面的“+”号去掉,括号里的各项都不变;括号前面是“-”号,把括号和它前面的“-”号去掉,括号里面的各项都要变号
(2)去括号是,括号前面的系数不是1,则要按分配律来计算,即要把括号外的系数乘以括号内的每一项
2. 添括号法则:
(1)所添括号前是“+”号,括号里面的各项都不变号;所添括号是“-”号,括号里面各项都要变号
3. 整式的加减运算,实际上就是合并同类项,在运算时,如果遇到括号,就根据去括号法则,先去括号,再合并同类项
注意:同类项和系数的大小没有关系
4.3整式的乘除
考点一:幂的运算(重点重点重点)
(1)同底数幂的乘法:同底数幂相乘,底数不变,指数相加,即am*an=am+n(m、n为整数)
(2)幂的乘方:幂的乘方,底数不变,指数相加,即(am)n=amn(m、n为整数)
(3)积的乘方:积的乘方,等于个因式乘方的根,即(ab)n=anbn(n为整数)
注意:

(4)同底数幂的除法:同底数幂相除,底数不变,指数相减,即am/an=am-n(m、n为整数)
(5)零指数幂:任何不为0的数的0次幂都是等于1,即a0=1(a≠0)
(6)负整数指数幂:任何不等于0的数的-n(n为整数)次幂,等于这个数的n次幂的倒数,即a-n=1/an(a≠0, n为整数)
考点二:整式的乘法运算
1.单项式乘单项式:单项式乘单项式,就是把他们的系数、同底数幂分别相乘,其余字母连同它们的指数作为积的一个因式。如:(-5a2b)*(-3a)=(-5)*(-3)(a2*a)*b=15a3b
2.单项式乘多项式:单项式乘多项式,就是用单项式去乘多项式的每一项,再把所得的积相加。如:m(a+b+c)=ma+mb+mc
注意:(1)单项式乘多项式的每一项时,不要漏项,因式中的多项式是几项,积就是几项
(2)计算时需要注意各项的符号
3. 多项式乘多项式:多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加。即(a+b)(m+n)=am+an+bm+bn
注意:(1)多项式乘以多项式的结果任然适多项式,在合并同类项之前,积的项数等于两个多项式项数的积
(2)结果中若有同类项,则要合并,所得结果必须为最简的形式
4.乘法公式:(非常重要,重点中的重点)
(1)平方差公式:(a+b)(a-b)=a2-b2反之也成立
平方差公式的特点:①左边是两个二项式相乘,且二项式中的两项有一项是相同的,另一项互为相反数
②右边是两项的平方差
③公式中的a和b可以是单项式,也可以是多项式
(2)完全平方公式:(a+b)2=a2+b2+2ab、(a-b)2=a2+b2-2ab
完全平方公式的特点:①记忆口诀;首平方,尾平方,2倍乘积在中央
②公式中的a和b可以是单项,也可以是多项
注意:(1)完全平方公式常见的变形
a2+b2=(a+b)2-2ab=(a-b)2+2ab
(a+b)2+(a-b)2=2(a2+b2)
(a+b)2-(a-b)2=4ab
考点三:整式的除法运算
1. 单项式除以单项式:单项式除以单项式,把系数、同底数幂分别相除,作为商的一个因式,对于只在被除式中含有的字母,则连同它的指数作为商的一个因式。
如:(-12a4b3c)/3a2b=-12/3*a4-2*b3-1*c=-4a2b2c
注意:(1)运算中的单项式的系数包括它前面的符号
(2)不要遗漏只在被除式中含有的字母
2.多项式除以单项式:多项式除以多项式,就是把多项式的每一项除以这个单项式,再把所得的商相加
如:(ma+mb+mc)/m=ma/m+mb/m+mc/m=a+b+c
考点四:整式的混合运算
1. 含有整式的加减、乘除及乘方的多种运算叫做整式的混合运算
2. 整式的混合运算顺序:先乘方,再乘除,后加减,有括号时先算括号里面的,去括号时,先去小括号,再去中括号,最后去大括号
4.4因式分解
考点一:因式分解
把一个多项式化成几个整式的乘积的形式,叫做这个多项式的因式分解。(这样子有可能有的同学没有办法看懂,其实可以理解为:因式分解就是把相加减的式子变成相乘)
考点二:因式分解的方法 重点重点步骤就是按下面的顺序来
1. 提公因式法:提取各项的公因式
2. 公式法:平方差公式和完全平方公式
3. 分组分解法:66.7%口诀,例:xy-x-y+1=(x-1)(y-1)(重点哦)
4. 十字相乘法:例 x2-2x-3,先把x2分成两个x,再把3分成-3和1,然后就等于(x-3)(x+1)
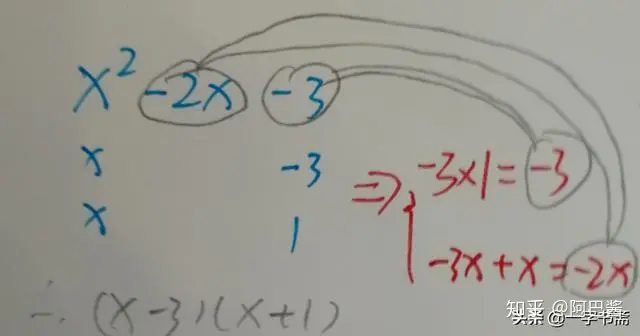
因式分解的一般步骤:“一提、二套、三试、四分、五查”
注意事项:(重点重点)
(1)分到不能分为止
(2)因式分解各项均只能用小括号连接
(3)因式分解每一项的首项系数为正
(4)因式分解中单项式写在多项式之前
(5)分解结果中有同类项的注意合并同类项
若首项系数是负数时,一般要把“-”提出来,使括号内的首项系数为正



