第一步，我们先看一张凸透镜成像的光路图：

如图，O为透镜光心，F为其一焦点，A点发出的光线AC过焦点F，经过凸透镜后平行于主光轴，AO经过透镜后方向不变，交射线AO于A'。则A的像在A'处，进而，AB的像就在A'B'处。我们要讨论的是物距OB、像距OB'、物的大小AB和像的大小A'B'的关系。

第二步：

我们先看一个特殊位置，当OF=FB，即OB=2OF时，

观察ΔCOF与ΔABF，

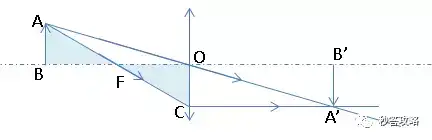
∵∠CFO=∠AFB(对顶角相等)

∠COF=∠ABF=Rt∠

OF=BF

∴RtΔCOF≌RtΔABF

∴AB=OC

∵A'C∥B'O

∴A'B'=CO

∴AB=AB'

即，此时像的大小等于物的大小。

类似地，观察ΔABO与ΔA'B'O，

易证：OB=OB'

即，此时像距等于物距。

至此，我们得到了一个结论：

当物距等于2倍焦距时，物距等于像距，物像同大小。

第三步：

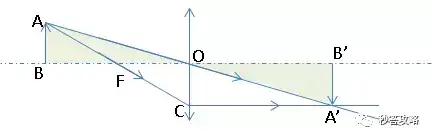
在前面的图中，若AB远离透镜，如图：

此时，OF

OC

故：

A'B'

即当物距大于2倍焦距时，物距大于像距，物大于像。

同时，我们还可以看出，OB'

即

物大物距大，像小像距小。也就是：谁远谁大。

第四步：

同样的方法，也可以证明当AB靠近透镜时，A'B'远离透镜，像变大。其实跟据光路可逆远离，也可以得到：若物体在A'B'处，其像必在AB处。

由图还可以推出，当B点与F点重合时，AF将于透镜平行，此时将无法成像。(这个点也是凸透镜成实像与成虚像的临界点。)

综上，我们可以得到凸透镜焦距、物距、像距、以及它们的大小关系如下：

当物距等于像距等于2倍焦距时，物像同大。当其中一个大于2倍焦距时，另一个在一倍焦距和2倍焦距之间。谁远谁大。

注1：从以上结论可以看出，凸透镜成实像时，物、像均在在透镜的焦点之外。

注2：以上证明过程使用了过光心光线和过焦点光线，其实用平行光线和过光心的光线同样可以得到以上结论。当物距小于透镜焦距时，利用平行光线和过光心的光线可以画出虚像的位置和大小，有兴趣可自行完成。

好了，有了以上结论，我们来做几道练习题，牛刀小试一把。

练习1. 将蜡烛放在离凸透镜36cm的地方，在离凸透镜12cm的光屏上可以得到烛焰的清晰的像，则凸透镜的焦距可能是( )。

A. 3cm B. 6cm C. 9cm D. 20cm

练习2. 将蜡烛放在离凸透镜30cm的地方，在离凸透镜45cm的光屏上可以得到烛焰的清晰的像，则

A.凸透镜的焦距是90cm，像是放大的。 B.凸透镜的焦距是18cm，像是放大的。

C.凸透镜的焦距是10cm，像是放大的。 D.凸透镜的焦距是10cm，像是缩小的。

练习3. 一物体放在凸透镜前20cm主光轴上，在光屏上能得到放大的像，据此可判断( )

A. 物体放在凸透镜前主光轴上21cm处，一定能得到放大的实像

B. 物体放在凸透镜前主光轴上21cm处，一定能得到缩小的实像

C. 物体放在凸透镜前主光轴上10cm处，一定能得到放大的虚像

D. 物体放在凸透镜前主光轴上19cm处，一定能得到缩小的实像

练习4. 一物体放在凸透镜前主光轴上，在光屏上能得到缩小的像，若要使像变大，物体位置不变，则应( )

A. 凸透镜靠近物体，同时增加光屏与透镜的距离

B. 凸透镜靠近物体，同时缩短光屏与透镜的距离

C. 凸透镜远离物体，同时增加光屏与透镜的距离

D. 凸透镜远离物体，同时缩短光屏与透镜的距离

练习5. 给凸透镜“戴”上近视眼镜，此时光屏上能成一清晰的像。若“取”下近视眼镜，为使光屏上的像清晰，在保持烛焰和透镜位置不变的条件下，应该将光屏 (　 )

A.靠近透镜 B.远离透镜

C.靠近透镜和远离透镜都可以 D.保持在原来的位置