三角形常见辅助线

1.在利用三角形三边关系证明线段不等关系时，如果直接证不出来，可连结两点或延长某边构造三角形，使结论中出现的线段在一个或几个三角形中，再利用三边关系定理及不等式性质证题.

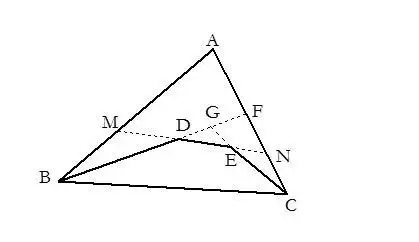
注意：利用三角形三边关系定理及推论证题时，常通过引辅助线，把求证的量(或与求证有关的量)移到同一个或几个三角形中去然后再证题.

2.在利用三角形的外角大于任何和它不相邻的内角证明角的不等关系时，如果直接证不出来，可连结两点或延长某边，构造三角形，使求证的大角在某个三角形外角的位置上，小角处在内角的位置上，再利用外角定理证题.

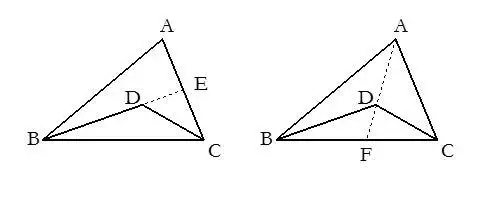
3.有角平分线时常在角两边截取相等的线段，构造全等三角形.

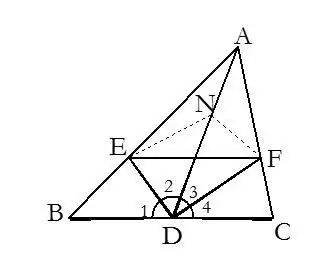
4. 有以线段中点为端点的线段时，常加倍延长此线段构造全等三角形.

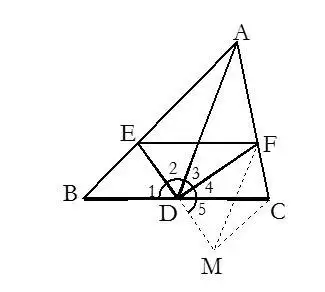
5.在三角形中有中线时，常加倍延长中线构造全等三角形.

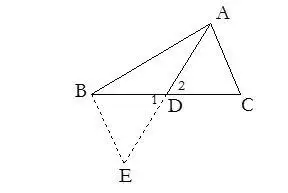
6.截长补短作辅助线的方法

截长法：在较长的线段上截取一条线段等于较短线段;

补短法：延长较短线段和较长线段相等.

这两种方法统称截长补短法.

当已知或求证中涉及到线段a、b、c、d有下列情况之一时用此种方法：

①a>b

②a±b = c

③a±b = c±d

7.证明两条线段相等的步骤：

①观察要证线段在哪两个可能全等的三角形中，然后证这两个三角形全等。

②若图中没有全等三角形，可以把求证线段用和它相等的线段代换，再证它们所在的三角形全等.

③如果没有相等的线段代换，可设法作辅助线构造全等三角形.

8.在一个图形中，有多个垂直关系时，常用同角(等角)的余角相等来证明两个角相等.

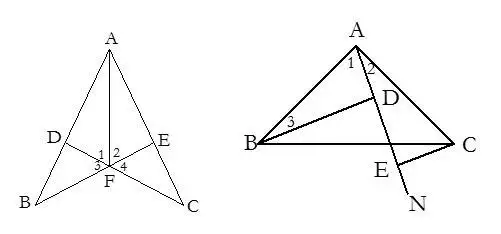
9.三角形一边的两端点到这边的中线所在的直线的距离相等.

10.条件不足时延长已知边构造三角形.

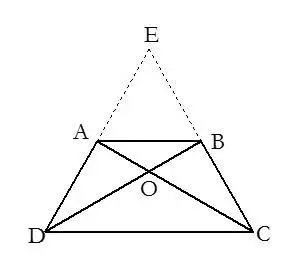
11.连接四边形的对角线，把四边形问题转化成三角形来解决问题.

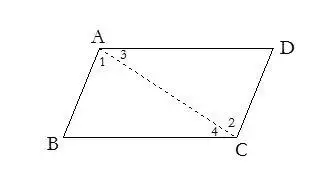
12.有和角平分线垂直的线段时，通常把这条线段延长。可归结为“角分垂等腰归”

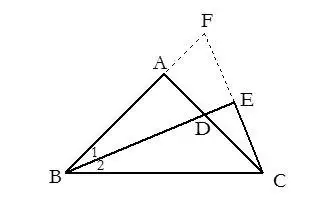
13.当证题有困难时，可结合已知条件，把图形中的某两点连接起来构造全等三角形。

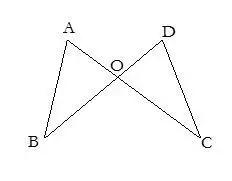
14.当证题缺少线段相等的条件时，可取某条线段中点，为证题提供条件.

例：已知，如图，AB = DC，∠A = ∠D

求证：∠ABC = ∠DCB

证明：分别取AD、BC中点N、M，

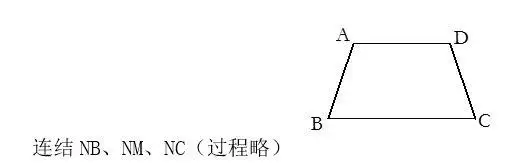
15.有角平分线时，常过角平分线上的点向角两边做垂线，利用角平分线上的点到角两边距离相等证题.

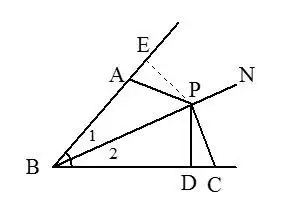
18.有垂直平分线时常把垂直平分线上的点与线段两端点连结起来.

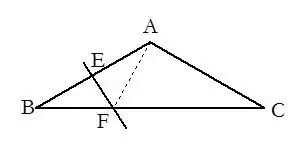
19.有垂直时常构造垂直平分线.

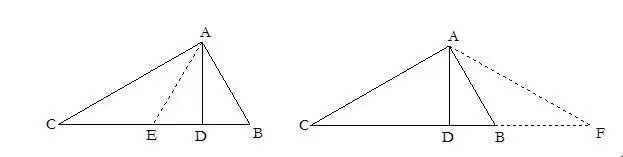
20.有中点时常构造垂直平分线.

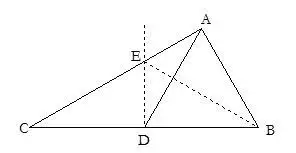
21.当涉及到线段平方的关系式时常构造直角三角形，利用勾股定理证题.

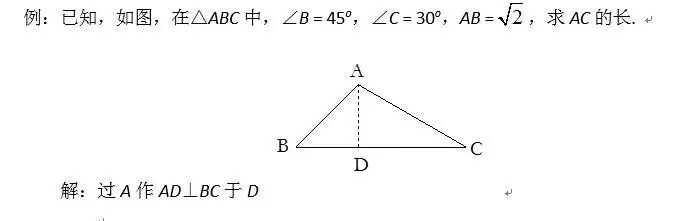
22.条件中出现特殊角时常作高把特殊角放在直角三角形中.

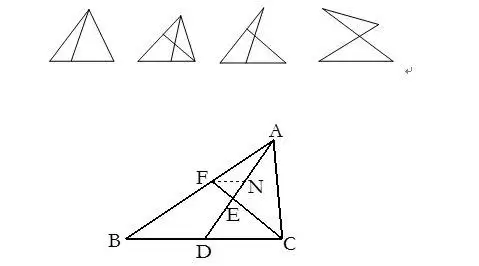
23.当图形中有叉线(基本图形如下)时，常作平行线.