在平面直角坐标系中，求一个三角形面积，需要根据三角形的各顶点的坐标，确定底与高，进而求出三角形面积。其它不规则的多边形经常通过割补转化成三角形或可以计算的四边形(矩形，梯形等)来计算面积。例如可以把四边形分割成两个三角形来计算(五边形可以分割成3个三角形，n边形可以分割成n-2个三角形)。所以最基础最重要的就是三角形面积的计算!

三角形的面积计算

(一)有边与坐标轴平行时，可以直接计算三角形面积。

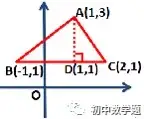
如上图，因为有边与坐标轴平行，所以这条边的长度，和这条边上的高就非常容易计算，底BC=2-(-1)=3，高AD=3-1=2，之后可以直接计算△ABC的面积。

(二)当三角形是一个斜三角形

①铅锤法(三角形面积=水平宽×铅锤高÷2)

过点A作AD垂直于x轴，交BC于点D，则AD叫做铅锤高。点D的横坐标与A相同，纵坐标可以利用直线AD与直线BC求得，之后可以得到AD的长度。

过点B与点C作x轴的垂线，两条垂线的距离叫做水平宽。

其原理就是把△ABC分割成两个以AD为底的两个三角形：△ABD与△CAD，它俩的高的和就是水平宽w，所以S△ABC=S△ABD+S△CAD=hw/2

②补成梯形，过三个顶点作x轴与y轴的垂线。

用S梯形ABDE-S△CEA-S△BDC

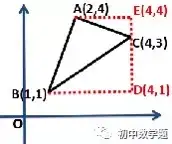
③也可以通过重组转化成直角梯形面积的和与差。例如下图，S△ABC=S梯形ABDE+S梯形CAEF-S梯形CBDF

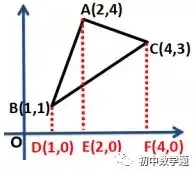
方法很多，可根据题的特点和已知条件来灵活选择解法。

多边形

(一)分割成三角形或可以计算的四边形(梯形等)

如图所示，四边形ABCD中，A(2，4)，B(1，2)，C(3，1)，D(5，3)，求四边形ABCD的面积。例如：S四边形ABCD=S△ABC+S△ACD

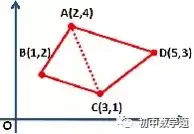
(二)也可以围补成可以计算的四边形，此处补成长方形再减去4个容易计算的直角三角形来计算。

把不规则图形转化成可以计算面积的规则图形时，最基本的方法就是割与补，方法不是唯一的，可根据题的特点灵活选择解法。

上面是坐标系下图形面积的基本计算方法，实际题目会结合函数来出题，例如我们学过的一次函数。如果有动点，可以化动为静，然后按照上面的基本方法把图形面积表示出来。