一次函数面积问题，在初二阶段绝大部分题目都是涉及三角形面积，主要分为求解图形面积和已知面积求点坐标或线解析式。其实这两类题目是相通的，都是要我们找出所求面积的表达式。

这类题目的解答方法比较灵活，常用方法包括直接求值法、割补法、等面积转换法、水平宽铅垂高法等。一般来说一道题都有多种方法，就看哪一种方法计算简便。

例题1：

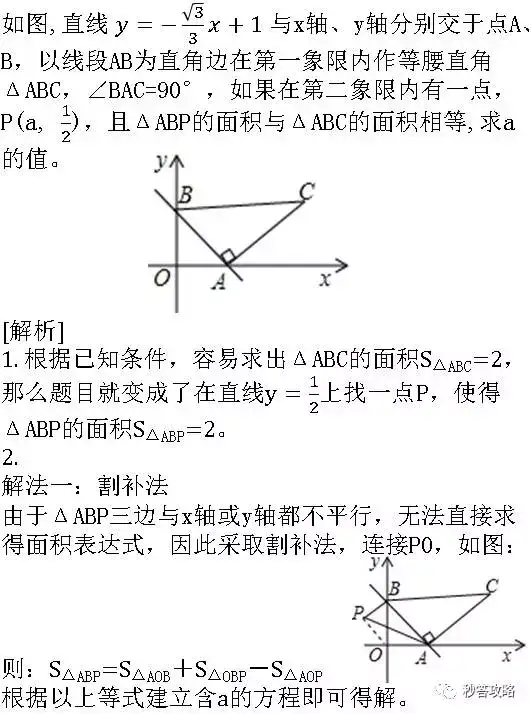
由上可以看出，此题使用第二种方法较为简单。关于水平宽解题法，请看这里：口算秒解高级2017秋期中压轴题第二问，三角形面积题的例题分析。

例题2：

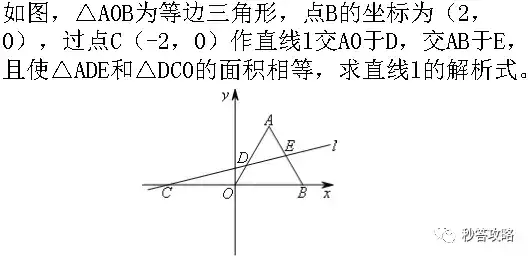
[思路解析]

此题的解法就更多了，最直接的解法就是分别设D、E的横坐标，根据面积相等和C、D、E在直线l上分别列出等式(方程)，计算求解。话说这个方法虽然直接，但是计算非常麻烦，所以不建议使用。下面给出两个相对简单的解法。

解法一：

由ΔADE与ΔODC面积相等，易得直线OE平行于直线CA(详解请看本讲的提示1)。据此可以得到直线OE的解析式，与直线AB的解析式连立可得E点坐标，此题得解。(由OE∥AC，又O是CB的中点，也可根据几何法得出E是线段AB的中点，得解。)

解法二：

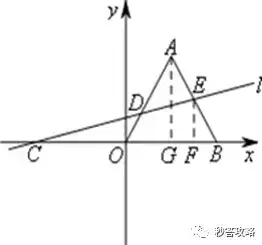
如图，由ΔADE和ΔDCO的面积相等得到ΔBCE和ΔABO的面积相等，又因为BC=2BO，故有AG=2EF，可得E点坐标。

通过以上两个例题可以看出，一次函数面积题的解题方法是非常灵活的，因此对于此类题目，我们不要急于列解析式求解，而应该通过观察和分析，采用割补、替换或者转换等方法，将已知的面积关系转化为点的位置关系或线段的长度关系，然后找到适合的简便解法。

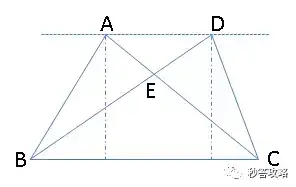
提示1：如图，若有ΔABE和ΔDEC面积相等，则ΔABC和ΔDBC面积相等。又因为两个三角形有一个公共底边BC，故两条高相等，因此，必有AD∥BC。

提示2：此类题目对知识点的考察比较综合，往往包括：一次函数图像性质(截距、斜率的含义)、距离公式、待定系数法、比例法等知识点和解题技巧。