三角形的中线是连接三角形顶点和它的对边中点的线段。每个三角形都有三条中线，它们都在三角形的内部，三条中线的交点是三角形的重心。这个点是各中线的三等分点。

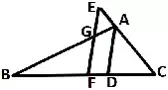
如图BE是∆ABC的AC边上的中线。根据中线的定义，可知中线与对边的交点是对边的中点，这就有了一个隐藏的等量关系，即AE=CE。

倍长中线

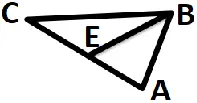
延长中线，使所延长部分与中线相等，然后连接相应的顶点，则对应角对应边都对应相等，可以构造全等三角形。

为了理解这种方法，我们把它补全成平行四边形。延长BE到点D使DE=BE，连接AD与CD，会得到一个平行四边形ABCD

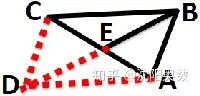
虽然初一还没有学习平行四边形，但是简单了解一下有助于我们理解倍长中线这种方法。

平行四边形的性质：平行四边形的两组对边分别相等;平行四边形的对角线互相平分。这些性质可以和倍长中线构造的全等三角形相互理解和验证。

作用：转化线段

上图中通过倍长中线，得到∆CDE≌∆ABE，可得CD=AB，这样可以把AB转化成CD，可以把不在同一个三角形的线段转到同一个三角形中。

例题1：如图∆ABC中，AB=5，AC=9，则BC边上的中线AD的长度的取值范围是多少。

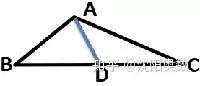
比较线段的大小或确定取值范围，可以利用三角形的三边关系：任意两边之和大于第三边，任意两边之差小于第三边。这样就需要比较的线段对象要在同一个三角形的，所以可以利用倍长中线来转化线段。

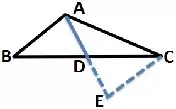
所以我们延长AD到点E使DE=AD，连接CE。

在∆ABD与∆ECD中，AD=ED，∠ADB=∠EDC，BD=CD，所以∆ABD≌∆ECD，所以AB=EC。把AB转化到EC，这样AC，EC，与中线AD就在同一个三角形中(此处AE=2AD)

然后根据三角形的三边关系，AC-EC

接下来我们看一下关于极限值2和7的情况。当∠A接近180°时，即B，A，C在一条直线时，BD=BC，此时AD=(AB+BC)/2 -AB=2。当∠A接近0°时，即A，B，C在一条直线时，BD=CD，此时AD=(AC-AB)/2 +AB=7

虽然动图比较直观，但是孩子们尽量试着自己想象一下它的变化过程。

在几何题中，只要有中点，我们就可以想到三角形中线，试着倍长中线来构造全等三角形(关于中点，我们就多了一个思路)。

下面这种图形，已知F是BC的中点，虽然BE没有连接，但是其实EF就是∆BCE的中线，可以倍长EF来构造全等三角形。例如延长EF到点H，使HF=EF，则有∆CEF≌∆BHF。