2022年初中数学用函数图象法秒解平面直角坐标系点坐标题目
2022-09-07 13:24:04佚名
 点击免费领取中考核心考点资料!
点击免费领取中考核心考点资料!
我们今天采用函数图象法秒解一道平面直角坐标系点坐标题目,例题本身比较简单,常规解法也不算太麻烦,因此秒解的意义只有一个,那就是“快!稳!”,题目如下:
无论m为何值,P(m-3,4-2m)不可能在第_________象限。
[常规思路解析]
①若点P在第一象限,则有m-3>0 且 4-2m>0,连立,m无解;
②若点P在第二象限,则有m-3<0 且 4-m>0,连立解得m<3;
③若点P在第三象限,则有m-3<0 且 4-2m<0,连立解得2
④若点P在第四象限,则有m-3>0 且 4-2m<0,连立解得m>3;
∴无论m为何值,P(m-3,4-2m)不可能在第一象限。
没毛病,根据已知的坐标代数式,按照四个象限分情况讨论,连立解不等式组,即可得到正确答案。这也是我在网上找到的本题的唯一解法。But... ...对于本题,秒答君想说,换个思路,海阔天空,请看秒答解析。
[解析]
1. 由题可知,点P的横、纵坐标均为m的函数,如果我们连立两个函数式,则可以求得点P的纵横坐标之间的关系。
也就是说,设P点坐标为(x,y),由题意,有
x=m-3,y=4-2m,连立消m,可得
y=-2x-2。
2. 可见,无论m为何值,点P都要满足这个关系式。即点P一定在直线
y=-2x-2上,
这是一条斜率为负、截距为负的直线,过二、三、四象限。因此,点P不可能在第一象限。
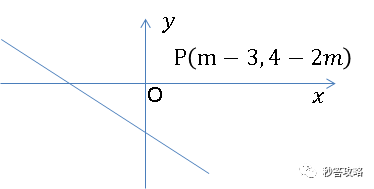
本题采用函数图象法比常规解法简便、快速、直观,有且具有更广泛的适应性,比如将此题变形,问点P能否在平面坐标系某一区域内,前面常规解法就更加麻烦,而函数图象法同样适用。



