2020初中数学平行四边形的性质知识点总结(二)
2020-05-29 08:52:57佚名
 点击免费领取中考核心考点资料!
点击免费领取中考核心考点资料!
知识点总结
一、特殊的平行四边形
1.矩形:
(1)定义:有一个角是直角的平行四边形。
(2)性质:矩形的四个角都是直角;矩形的对角线平分且相等。
(3)判定定理:
①有一个角是直角的平行四边形叫做矩形。②对角线相等的平行四边形是矩形。③有三个角是直角的四边形是矩形。
直角三角形的性质:直角三角形中所对的直角边等于斜边的一半。
2.菱形:
(1)定义 :邻边相等的平行四边形。
(2)性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
(3)判定定理:
①一组邻边相等的平行四边形是菱形。
②对角线互相垂直的平行四边形是菱形。
③四条边相等的四边形是菱形。
(4)面积: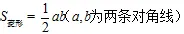
3.正方形:
(1)定义:一个角是直角的菱形或邻边相等的矩形。
(2)性质:四条边都相等,四个角都是直角,对角线互相垂直平分。 正方形既是矩形,又是菱形。
(3)正方形判定定理:
①对角线互相垂直平分且相等的四边形是正方形;
②一组邻边相等,一个角为直角的平行四边形是正方形;
③对角线互相垂直的矩形是正方形;
④邻边相等的矩形是正方形
⑤有一个角是直角的菱形是正方形;
⑥对角线相等的菱形是正方形。
二、矩形、菱形、正方形与平行四边形、四边形之间的联系:
1.矩形、菱形和正方形都是特殊的平行四边形,其性质都是在平行四边形的基础上扩充来的。矩形是由平行四边形增加“一个角为90°”的条件得到的,它在角和对角线方面具有比平行四边形更多的特性;菱形是由平行四边形增加“一组邻边相等”的条件得到的,它在边和对角线方面具有比平行四边形更多的特性;正方形是由平行四边形增加“一组邻边相等”和“一个角为90°”两个条件得到的,它在边、角和对角线方面都具有比平行四边形更多的特性。
2.矩形、菱形的判定可以根据出发点不同而分成两类:一类是以四边形为出发点进行判定,另一类是以平行四边形为出发点进行判定。而正方形除了上述两个出发点外,还可以从矩形和菱形出发进行判定。
三、判定一个四边形是特殊四边形的步骤:
常见考法
(1)利用菱形、矩形、正方形的性质进行边、角以及面积等计算;
(2)灵活运用判定定理证明一个四边形(或平行四边形)是菱形、矩形、正方形;
(3)一些折叠问题;
(4)矩形与直角三角形和等腰三角形有着密切联系、正方形与等腰直角三角形也有着密切联系。所以,以此为背景可以设置许多考题。
误区提醒
(1)平行四边形的所有性质矩形、菱形、正方形都具有,但矩形、菱形、正方形具有的性质平行四边形不一定具有,这点易出现混淆;
(2)矩形、菱形具有的性质正方形都具有,而正方形具有的性质,矩形不一定具有,菱形也不一定具有,这点也易出现混淆;
(3)不能正确的理解和运用判定定理进行证明,(如在证明菱形时,把四条边相等的四边形是菱形误解成两组邻边相等的四边形是菱形);(3)再利用对角线长度求菱形的面积时,忘记乘;(3)判定一个四边形是特殊的平行四边形的条件不充分。
【典型例题】(2010天门、潜江、仙桃)正方形ABCD中,点O是对角线DB的中点,点P是DB所在直线上的一个动点,PE⊥BC于E,PF⊥DC于F.
(1)当点P与点O重合时(如图①),猜测AP与EF的数量及位置关系,并证明你的结论;
(2)当点P在线段DB上 (不与点D、O、B重合)时(如图②),探究(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)当点P在DB的长延长线上时,请将图③补充完整,并判断(1)中的结论是否成立?若成立,直接写出结论;若不成立,请写出相应的结论.
【解析】(1)AP=EF,AP⊥EF,理由如下:
连接AC,则AC必过点O,延长FO交AB于M;
∵OF⊥CD,OE⊥BC,且四边形ABCD是正方形,
∴四边形OECF是正方形,
∴OM=OF=OE=AM,
∵∠MAO=∠OFE=45°,∠AMO=∠EOF=90°,
∴△AMO≌△FOE,
∴AO=EF,且∠AOM=∠OFE=∠FOC=45°,即OC⊥EF,
故AP=EF,且AP⊥EF.
(2)题(1)的结论仍然成立,理由如下:
延长AP交BC于N,延长FP交AB于M;
∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,
∴四边形MBEP是正方形,
∴MP=PE,∠AMP=∠FPE=90°;
又∵AB-BM=AM,BC-BE=EC=PF,且AB=BC,BM=BE,
∴AM=PF,
∴△AMP≌△FPE,
∴AP=EF,∠APM=∠FPN=∠PEF
∵∠PEF+∠PFE=90°,∠FPN=∠PEF,
∴∠FPN+∠PFE=90°,即AP⊥EF,
故AP=EF,且AP⊥EF.
(3)题(1)(2)的结论仍然成立;
如右图,延长AB交PF于H,证法与(2)完全相同



