2020初中数学实际问题中的不等式组
2020-05-25 10:49:08佚名
 点击免费领取中考核心考点资料!
点击免费领取中考核心考点资料!
学习了一元一次不等式组以后,我们可以利用不等式组解决许多与实际密切联系的问题。解决此类问题的关键是要找准不等关系,从而根据不等关系列出不等式组把问题解决。一般情形下,在有关一元一次不等式组的实际问题中,不等关系分为两种类型。
一、不等关系明显型
此类问题的特点是在题目中会出现明显的表示不等关系的关键字,如“大于”、“小于”、“不能超过”、“不少于”、“最多”等。
例1 (哈尔滨市)双蓉服装店老板到厂家选购A、B两种型号的服装,若销售一件A型服装可获利18元,销售一件B型服装可获利30元,根据市场需求,服装店老板决定,购进A型服装的数量要比购进B型服装数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后,可使总获利不少于699元,问有几种进货方案?如何进货?
分析:由题意,本题不等关系非常明显,由两个表示不等关系的关键字即可看出,即“最多”和“不少于”,因此要解决本题我们可以直接根据这两个关键字列出不等式组。
解:设B型服装购进x件,则A型服装购进件,根据题意,得
解得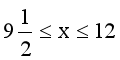
因为x为整数,所以x=10、11、12
所以、26、28
所以有三种进货方案:B型服装购进10件,A型服装购进24件或B型服装购进11件,A型服装购进26件;B型服装购进12件,A型服装购进28件。
例2 (连云港市)光明农场有某种植物10000千克,打算全部用于生产高科技药品和保健食品。若生产高科技药品,1千克该植物可提炼出0.01千克的高科技药品,将产生污染物0.1千克,每1千克高科技药品可获利润5000元;每生产1千克保健食品可获利润100元。1千克该植物可生产0.2千克保健食品,将产生污染物0.04千克。要使总利润不低于410000元,所产生的污染物总量不超过880千克,求用于生产高科技药品的该植物重量的范围。
分析:由题意很容易发现体现本题不等关系的两个关键字,即“不低于”和“不超过”,因此我们就根据这两个关键字列出不等式组把问题解决。
解:设用于生产高科技药品的该植物重量为x千克,则用于生产保健食品的该植物重量为(10000-x)千克,根据题意,得
解得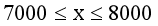
所以用于生产高科技药品的该植物重量不低于7000千克且不高于8000千克。
二、不等关系隐含型
此类问题的特点是题目中没有出现表示不等关系的关键字,因此不等关系比较含蓄,需要我们从题意中分析得到。
例3 (广东省茂名市)今年6月份,我市某果农收获荔枝30吨,香蕉13吨,现计划租用甲、乙两种货车共10辆,将这批水果全部运往深圳,已知甲种货车可装荔枝4吨和香蕉1吨,乙种货车可装荔枝、香蕉各2吨。
(1)该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来。
(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,则该果农应选择哪种方案使运输费最少?最少运输费是多少?
分析:本题没有明显的不等关系,但是从题意可知本题是一个最优方案设计问题,因此可以建立不等式组模型来解决问题。由题意,本题的不等关系为:10辆甲、乙两种货车的运货总量至少要达到30吨荔枝,13吨香蕉。
解:(1)设安排甲种货车x辆,则安排乙种货车(10-x)辆,根据题意,可得
因为x为整数,所以x=5、6、7,
所以5、4、3。
所以车辆安排有三种方案:
方案一:甲种车、乙种车各5辆;
方案二:甲种车6辆、乙种车4辆;
方案三:甲种车7辆、乙种车3辆。
(2)方案一,要运输费:
方案二,要运输费:
方案三,要运输费
这说明,方案一所需运输费最少,为16500元。
例4 (常州市)七(2)班有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36千克,乙种制作材料29千克,制作A、B两种型号的陶艺品用料情况如下表:
需甲种材料 需乙种材料
1件A型陶艺品 0.9千克 0.3千克
1件B型陶艺品 0.4千克 1千克
(1)设制作B型陶艺品x件,求x的取值范围;
(2)请你根据学校现有材料,分别写出七(2)班制作A型和B型陶艺品的件数。
分析:本题题目中没有出现明显的表示不等关系的字,所以不等关系比较隐含,分析题意可发现,制作两种型号的陶艺品的材料已给出限制,所用材料不能超过这个限制,因此我们就可以根据总材料的限制来列出本题的不等式组。
解:(1)设制作B型陶艺品x件,则制作A型陶艺品为(50-x)件,由题意,得
解得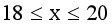
(2)由(1)知,又因为x为整数,
所以x=18、19、20,50-x=32、31、30
所以七(2)班制作A型和B型陶艺品的件数有三种可能:
可能一:制作A型陶艺32件,B型陶艺18件;
可能二:制作A型陶艺31件,B型陶艺19件;
可能三:制作A型陶艺30件,B型陶艺20件。



