考点：抛物线与x轴的交点；二次函数的性质．2448894

　　分析：如图，过点P作PE⊥x轴于点E．将△PAC的面积转化为S△PAC=S梯形OCPE﹣S△OAC﹣S△PAE．

　　解答：解：∵二次函数的解析式为，且该函数图象与x轴交于A、B两点，A在B点的左边，与y轴交于C点，

　　∴当y=0时，=0，

　　解得x1=1，x2=3，即A（1，0），B（3，0）．

　　当x=0时，y=2，即C（0，2）．

　　∴OC=2，OA=1，OB=3，AB=2．

　　如图过点P作PE⊥x轴于点E．设P点的坐标（x，）（x＞0）．

　　则S△PAC=S梯形OCPE﹣S△OAC﹣S△PAE=（+2）x﹣×1×2﹣×（x﹣1）（）=4．

　　即x2﹣x﹣12=0，

　　解得x=﹣3（舍去），或x=4．

　　当x=4时，y=2．

　　∴P点坐标是（4，2）．

　　答：P点坐标是（4，2）．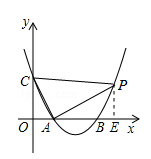

　　点评：本题考查了抛物线与x轴的交点，二次函数的性质．解答该题时，注意转化思想的应用．