点击免费领取中考核心考点资料！

　　考点：圆内接四边形的性质；平行四边形的性质．

　　分析：由四边形OABC为平行四边形，根据平行四边形对角相等，即可得∠B=∠AOC，由圆周角定理，可得∠AOC=2∠ADC，又由内接四边形的性质，可得∠B+∠ADC=180°，即可求得∠B=∠AOC=120°，∠ADC=60°，然后又三角形外角的性质，即可求得∠OAD+∠OCD的度数．

    

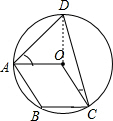
　　解答：解：∵四边形ABCD是圆内接四边形，

　　∴∠B+∠D=180°．

　　∵四边形OABC为平行四边形，

　　∴∠AOC=∠B．

　　又∵由题意可知∠AOC=2∠ADC．

　　∴∠ADC=180°÷3=60°．

　　连接OD，可得AO=OD，CO=OD．

　　∴∠OAD=∠ODA，∠OCD=∠ODC．

　　∴∠OAD+∠OCD=∠ODA+∠ODC=∠D=60°．

　　点评：此题考查了圆周角定理、圆的内接四边形的性质、平行四边形的性质以及三角形外角的性质．此题难度适中，注意数形结合思想的应用，注意辅助线的作法．