点击免费领取中考核心考点资料！

　　考点：全等三角形的判定与性质；平行线的性质．

　　分析：（1）根据各线段之间的长度，先猜想AD+BE=AB．

　　（2）在AB上截取AG=AD，连接CG，利用三角形全等的判定定理可判断出AD=AG．同理可证，BG=BE，即AD+BE=AB．

　　（3）画出直线l与直线MA不垂直且交点D、E在AB的异侧时的图形，分两种情况讨论：

　　①当点D在射线AM上、点E在射线BN的反向延长线上时；

　　②点D在射线AM的反向延长线上，点E在射线BN上时；

　　AD，BE，AB之间的关系．

　　解答：解：（1）AD+BE=AB．

　　（2）成立．

　　（方法一）：

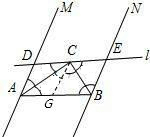
    在AB上截取AG=AD，连接CG．

　　∵AC平分∠MAB，

　　∴∠DAC=∠CAB，

　　又∵AC=AC，AD=AG，

　　∴△ADC≌△AGC（SAS），

　　∴∠DCA=∠ACG，

　　∵AM∥BN，

　　∴∠DAC+∠CAB+∠GBC+∠CBE=180°，

　　∵∠DAC=∠CAB，∠GBC=∠CBE，

　　∴∠CAB+∠GBC=90°，

　　∴∠ACB=90°即∠ACG+∠GCB=90°，

　　∵∠DCA+∠ACG+∠GCB+∠BCE=180°，

　　∴∠DCA+∠BCE=90°，

　　∴∠GCB=∠ECB，

　　∵∠ABC=∠CBE，BC=BC，

　　∴△BGC≌△BEC．

　　∴BG=BE，

　　∴AD+BE=AG+BG，AD+BE=AB．

　　（方法二）：

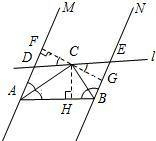
    过点C作直线FG⊥AM，垂足为点F，交BN于点G．作CH⊥AB，垂足为点H．

　　由（1）得AF+BG=AB，

　　∵AM∥BN，∠AFG=90°，

　　∴∠BGF=∠FGE=90°，

　　∵∠DAC=∠CAB，∠ABC=∠CBE，

　　∴CF=CH，CH=CG，

　　∴CF=CG，

　　∵∠FCD=∠ECG，

　　∴△CFD≌△CGE．

　　∴DF=EG，

　　∴AD+BE=AF+BG=AB．

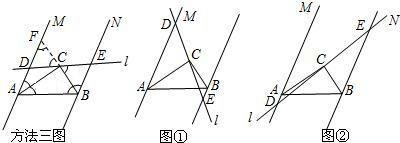
　　（方法三）：延长BC，交AM于点F．

　　∵AM∥BN，

　　∴∠FCD=∠CBG，

　　∵∠CBH=∠CBG，

　　∴∠FCD=∠CBH，

　　∴AF=AB，

　　∵∠DAC=∠CAB，AC=AC，

　　∴△AFC≌△ABC，CF=CB，

　　∵∠ECG=∠BCG，

　　∴△FCD≌△BCE，

　　∴DF=BE，

　　∴AD+BE=AD+DF=AF=AB．

　　（3）不成立．

　　存在．当点D在射线AM上、点E在射线BN的反向延长线上时（如图①），AD-BE=AB．

　　当点D在射线AM的反向延长线上，点E在射线BN上时（如图②），BE-AD=AB．

   

　　点评：此题很复杂，解答此题的关键是作出辅助线，利用全等三角形的判定定理及性质解答，解答（3）时注意分两种情况讨论，不要漏解．