考点：全等三角形的判定与性质；等边三角形的性质；旋转的性质．

　　分析：（1）根据等边三角形的性质可得AB=AD，AE=AC，∠BAD=∠CAE=60°，然后求出∠BAE=∠DAC，再利用"边角边"证明△BAE和△DAC全等，根据全等三角形对应边相等即可得证；

　　（2）①求出∠DAE，即可得到旋转角度数；

　　②当AC=2AB时，△BDD′与△CPD′全等．根据旋转的性质可得AB=BD=DD′=AD′，然后得到四边形ABDD′是菱形，根据菱形的对角线平分一组对角可得∠ABD′=∠DBD′=30°，菱形的对边平行可得DP∥BC，根据等边三角形的性质求出AC=AE，∠ACE=60°，然后根据等腰三角形三线合一的性质求出∠PCD′=∠ACD′=30°，从而得到∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PD′C=30°，然后利用"角边角"证明△BDD′与△CPD′全等．

　　解答：（1）证明：∵△ABD和△ACE都是等边三角形．

　　∴AB=AD，AE=AC，∠BAD=∠CAE=60°，

　　∴∠BAD+∠DAE=∠CAE+∠DAE，

　　即∠BAE=∠DAC，

　　在△BAE和△DAC中，

　　AB＝AD

　　∠BAE＝∠DAC

　　AE＝AC

　　∴△BAE≌△DAC（SAS），

　　∴BE=CD；

　　（2）解：①∵∠BAD=∠CAE=60°，

　　∴∠DAE=180°-60°×2=60°，

　　∵边AD′落在AE上，

　　∴旋转角=∠DAE=60°；

　　②当AC=2AB时，△BDD′与△CPD′全等．

　　理由如下：由旋转可知，AB′与AD重合，

　　∴AB=BD=DD′=AD′，

　　∴四边形ABDD′是菱形，

　　

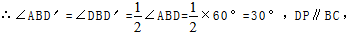
　　∵△ACE是等边三角形，

　　∴AC=AE，∠ACE=60°，

　　∵AC=2AB，

　　∴AE=2AD′，

　　

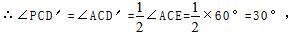
　　∴∠ABD′=∠DBD′=∠BD′D=∠ACD′=∠PCD′=∠PD′C=30°，

　　在△BDD′与△CPD′中，

　　∠DBD′＝∠PCD′

　　BD′＝CD′

　　∠BD′D＝∠PD′C

　　∴△BDD′≌△CPD′（ASA）．

　　故答案为：60．

　　点评：本题考查了全等三角形的判定与性质，等边三角形的性质，以及旋转的性质，综合性较强，但难度不大，熟练掌握等边三角形的性质与全等三角形的判定时提到过．