2012中考数学加油站:10月18日每日一题精练精析
2011-10-18 11:25:11张晖
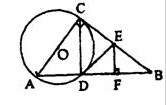
已知:如图△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,过D作⊙O的切线交BC于点E,EF⊥AB,垂足为F.
求证:(1)2DE=BC;
(2)若AC=6,BC=8,求S△ACD:S△EDF的值.
晖老师分析
考点:切线长定理;勾股定理.
分析:(1)根据题意可知:EC、ED均是圆O的切线,根据切线长定理可得出EC=DE,∠ECD=∠EDC;根据等角的余角相等,可得出∠EDB=∠B,因此DE=BE,
由此可得出DE=EC=BE, 由此可得证;
(2)由(1)知:DE=BE,因此DF=BF,根据等高的三角形面积比等于底边比可得出△EDF的面积是△EDB的面积的一半,同理可得出△EDB的面积是△CDB的面积的一半,
因此△EDF的面积是△CDB的面积的四分之一.那么本题只需得出△ADC和△CDB的面积比即可,即得出AD:BD的值即可.

作者介绍:
张晖:学而思初中数学核心教师,执教7年,拥有4年毕业班教学经验,总结了一套针对中考数学实用有效的教学方法。讲课思路清晰、幽默、具有亲和力,能够准确抓住学生心理,调动学生学习积极性.点击报班
相关阅读:



